Um carro de massa descreve sem derrapar uma curva no plano horizontal de raio com velocidade . O gráfico ao lado indica o comportamento da força de atrito para este caso específico.
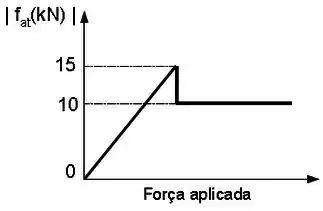
(c) Determine os coeficientes de atrito estático e cinético entre o carro e a pista.
Passo 1
Analisar o movimento do carro
Antes de mais nada, vamos das uma olhada no movimento do carro:
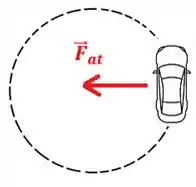
No movimento circular do carro, a nossa querida força de atrito vai atuar como uma força centrípeta, beleza? Se é assim, podemos igualar as duas:
Passo 2
(c) Análise gráfica
Antes do carro derrapar, a força de atrito vai crescendo até seu valor máximo. Depois, a força de atrito passa a ser constante com a força aplicada.
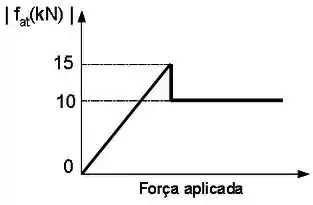
Então temos duas regiões no gráfico e para cada uma delas, vamos ter essas duas expressões meigas para a força de atrito:
Passo 3
Partir pras contas
Pô, da uma olhada no que as expressões da força de atrito tem em comum: a força normal! Como essa questão não tem nenhuma pegadinha nem nada, a força normal nesse caso vai se igualar ao peso do carro mesmo, logo:
Agora é só substituir! Falta saber qual força de atrito usar só. Eai, já sabe? Temos que usar antes de derrapar a força de atrito máxima e depois de derrapar a força de atrito pra quando o gráfico é constante, beleza? Partiu calcular agora:
Resposta
c)