Numa estrada horizontal o módulo da velocidade máxima com que um carro pode fazer uma certa curva circular sem derrapar é igual a . Se num dia de inverno, em razão da presença de gelo na pista, o coeficiente de atrito estático entre os pneus do carro e a estrada fica reduzido à metade, o módulo da velocidade máxima com que o carro pode fazer a mesma curva sem derrapar é igual a
(a)
(b)
(c)
(d)
(e)
Passo 1
A gente tem que tentar transformar esse enunciado em algo que a gente saiba lidar. No caso, o carro faz uma curva circular, então nesse instante, podemos considerar que o carro está seguindo um movimento circular.
Passo 2
Vamos considerar o plano da estrada, que é horizontal.
Os pneus do carro não derrapam, então o atrito entre eles e o asfalto é estático. Mas quando o carro está indo na velocidade , eles estão na iminência de derrapar, então a força de atrito estático é máxima. Podemos calcular o seu módulo assim:
sendo o coeficiente de atrito estático e o módulo da força normal que a estrada faz no carro.
Passo 3
Repare que, no plano da estrada, a única força atuando no carro é justamente a força de atrito estático máximo. O carro tem tendência a sair da curva, mas a , apontando pra dentro da curva, o mantém nela:
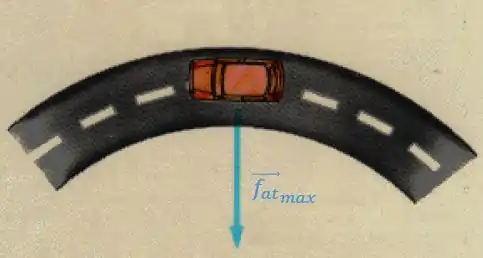
Passo 4
Então a força resultante na direção centrípeta é a . Sendo a massa do carro e a sua aceleração centrípeta, pela 2ª lei de Newton, temos
Passo 5
E o módulo da aceleração centrípeta é dado por:
onde é o raio da curva.
Passo 6
Ou seja,
Então essa é a expressão do coeficiente de atrito estático num dia comum, onde a velocidade máxima pra não haver derrapagem na curva é .
Passo 7
Agora vamos ver o caso da questão. Num dia de inverno, por causa do gelo, o coeficiente de atrito estático entre os pneus do carro e a pista é reduzido pela metade.
Vamos chamar esse novo coeficiente de atrito estático de . Então temos:
Ou seja,
Passo 8
Vamos chamar a nova força de atrito estático máximo de . Assim
Passo 9
A nova aceleração centrípeta vai ser , de módulo . E podemos chamar a nova velocidade máxima com que o carro pode fazer a curva sem derrapar de (o objetivo da questão é achar ). Assim,
Passo 10
Então fazendo exatamente a mesma coisa que antes, pela 2ª lei de Newton:
Passo 11
Show, então obtivemos:
Igualando as 2 expressões:
Multiplicando por dos 2 lados:
Demorou mas foi! :D
Resposta
Alternativa (a)