Um disco de metal de massa está ligado a um cubo de massa através de um fio que passa por um furo no centro de uma mesa, conforme mostrado na figura.
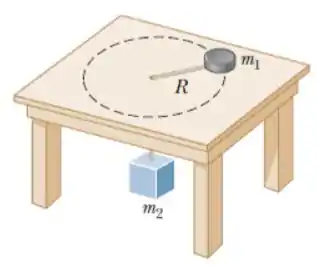
A superfície da mesa é perfeitamente lisa. O fio não tem massa e é inextensível. Considere . Você pode dar o resultado aproximado com uma casa decimal.
LEMBRETE: Todos os seus passos devem ser explicitados de forma clara.
- Suponha inicialmente que o movimento do disco é apenas radial, ou seja, na direção do fio. Qual será a aceleração do cubo? Você deve dar o módulo, a direção e o sentido do vetor aceleração.
- Ainda na situação de movimento apenas radial, determine a tração na extremidade do fio presa ao cubo?
- Suponha agora que o disco esteja descrevendo um movimento circular sobre a mesa ao longo de uma circunferência de raio . Qual deverá ser a velocidade do disco para que o cubo permaneça em repouso?
Passo 1
a)
Primeiramente vamos desenhar o diagrama de forças em cada objeto:
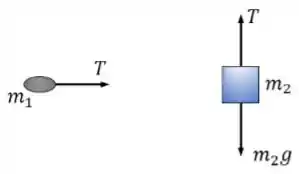
Agora, aplicamos a segunda lei de Newton para cada corpo. Escolhendo um eixo orientado na direção horizontal apontando para o furo da mesa.
Para o disco:
Escolhendo um eixo vertical orientado para baixo.
Para o bloco:
Por fim usamos o vínculo entre o bloco e o disco, por estarem ligados por um fio, os dois corpos devem ter a mesma velocidade e mesma aceleração :
Agora basta substituir a equação para a tração que encontramos analisando o disco na equação do bloco.
Este é o módulo do vetor aceleração do bloco. O vetor aceleração do bloco tem a direção vertical e aponta para baixo.
Passo 2
b)
Basta substituir o valor que encontramos para a aceleração na equação para a tração que encontramos para o disco:
Passo 3
c)
O disco descreve um movimento circular de velocidade constante e raio , cuja força resultante é a força de tração, assim como nos itens anteriores. Entretanto, essa força é agora a força centrípeta que produz o movimento circular do disco.
Analisando o disco:
Analisando o bloco:
Como o bloco está em repouso:
Substituindo:
Resposta
a)
b)
c)