Um disco está preso a um fio cujo comprimento é , e realiza um movimento circular sobre uma mesa de altura em relação ao solo. O fio arrebenta e o disco é lançado horizontalmente, atingindo o solo após um deslocamento horizontal de em relação ao ponto em que o disco deixa a mesa. Qual é o módulo da aceleração centrípeta do disco antes de o fio arrebentar? Despreze o atrito entre o disco e a mesa e use que .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Temos a seguinte situação:

No momento em que o fio arrebenta, esse disco vai sair com sua velocidade na direção tangencial e cair da mesa realizando um lançamento horizontal.
Queremos saber a aceleração centrípeta enquanto ele ainda realiza o movimento circular (antes do fio arrebentar).
A aceleração centrípeta é dada por:
Se já temos o raio do círculo (comprimento do fio), basta achar a velocidade. Sendo essa velocidade a mesma com que o disco é lançado da mesa.
Passo 2
Para resolver essa questão, vamos começar analisando o lançamento horizontal para achar a velocidade horizontal do disco.
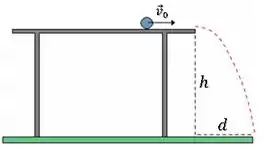
No lançamento horizontal vamos ter dois movimentos independentes.
Um movimento uniforme na horizontal, dado por:
Vamos chamar sua velocidade de e temos que seu deslocamento horizontal é :
O outro movimento é o de movimento uniformemente variado (queda livre). Temos a altura que o objeto cai e a aceleração da gravidade . Logo, temos:
Vamos chamar o tempo de queda de :
Se temos que o movimento durou , conseguimos achar a velocidade inicial do disco:
Passo 3
Agora que já temos a velocidade do disco, podemos calcular a aceleração centrípeta:
A velocidade é e o raio é o comprimento do fio :
Logo, a alternativa correta é (i).
Resposta
Letra (i)