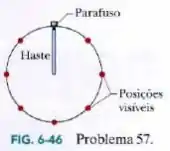
Um parafuso está enroscado em uma das extremidades de uma haste fina horizontal que gira em torno de outra extremidade. Um engenheiro monitora o movimento iluminando o parafuso e a haste com uma lâmpada estroboscópica, ajustando a frequência dos lampejos até o parafuso parecer estar nas mesmas oito posições a cada rotação completa da haste (Fig. 6-46). A frequência dos lampejos é por segundo, a massa do parafuso é e a haste tem de comprimento. Qual é o módulo da força exercida pela haste sobre o parafuso?
Passo 1
Neste movimento circular, temos a haste realizando a tração que faz o parafuso continuar na trajetória, por isso, temos que:
Sabemos também que a força centrípeta é dada por:
A massa nos foi dada e o raio da trajetória é o comprimento da haste, que também nos foi dado. O que nos falta, é a velocidade que o parafuso se movimenta.
Passo 2
Nos foi dado:
- Número de piscadas por segundo:
- Número de piscadas por volta:
É interessante para nós descobrir a frequência do movimento, ou seja, o número de voltas por segundo, certo? Então vamos analisar as unidades dos dados que nos foi dado... Se dividirmos o primeiro pelo segundo dado temos:
Com a frequência do movimento, conseguimos obter a velocidade angular:
Pra finalmente obtermos a velocidade linear:
Passo 3
Com o valor da velocidade encontrado, podemos voltar com ele para a expressão da força centrípeta:
Substituindo os valores de , e :