Um carro de massa trafega pelo topo de um morro de raio de curvatura com uma velocidade de módulo constante , conforme a figura. Considere .
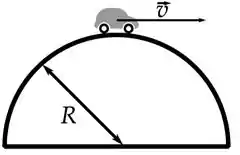
(a) Tratando o carro como uma partícula pontual e desconsiderando forças de atrito, represente diagramaticamente todas as forças que atuam sobre o carro quando ele está no topo do morro. Caso exista uma força resultante neste movimento, represente-a separadamente.
(b) Qual é o módulo da força normal que atua sobre o carro quando ele está no topo do morro a uma velocidade ?
(c) A que velocidade o carro está na iminência de perder o contato com o solo?
Passo 1
Como o nosso carrinho anda com velocidade constante, ele está realizando um Movimento Circular Uniforme.
Uma das características principais desse movimento é que a força resultante sobre o corpo deve atuar como Força Centrípeta, apontando para o centro da trajetória circular.
Vamos aos itens...
Passo 2
Na letra (a), queremos um diagrama de forças sobre o carro, considerando que não há atrito. Além disso, queremos separadamente a força resultante.
Quais são as forças atuando sobre ele?
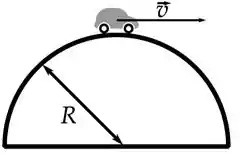
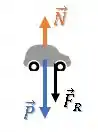
Temos uma força peso atuando para baixo e uma força normal atuando perpendicular à superfície, ou seja, para cima.
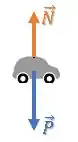
Mas olha aqui, e a força resultante ?
Será que essas duas forças têm o mesmo módulo, zerando a força resultante, ou será que uma é maior que a outra?
Passo 3
Se esse carrinho estivesse andando no plano, ele estaria realizando um movimento retilíneo uniforme, certo?
Então a força resultante sobre ele seria nula, já que ele não sofre nenhuma aceleração.
Porémmm, o carro está realizando um movimento circular, então, há uma força resultante atuando sobre ele.
Vimos lá no Passo 1 que é a força centrípeta e essa força atua para o centro do círculo.
Se a força resultante está para baixo, a resposta é que a força peso é maior que a força normal:
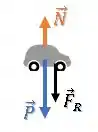
Passo 4
Na letra (b), queremos achar a força normal se a velocidade do carro é de .
Usando o diagrama de forças que achamos, temos que:
E além disso, sabemos que a força resultante atua como força centrípeta, então podemos usar a expressão para essa força:
A força peso é dada por :
Substituindo os valores, temos:
Passo 5
Na letra (c), queremos saber a velocidade que faz o carro estar prestes a perder o contato com o solo.
Como é que fazemos isso?
Bom, na iminência de perder o contato, o pneu do carro está quaaaase desencostando do chão, ou seja, a sua força de contato chega a zero:
Então, basta substituirmos esse valor e encontrar :
Cortando :
Resposta
(a)
(b)
(c)