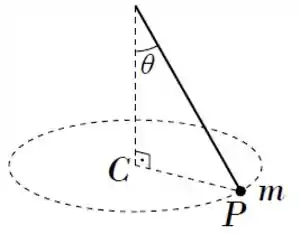
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal que faz um ângulo com a vertical, de modo que a partícula esteja em movimento circular uniforme em um plano horizontal com o centro da trajetória no ponto da vertical, como indica a figura. Em um dado instante, em que a partícula está em um ponto , sua aceleração é um vetor de
(a) módulo , vertical apontando pra baixo
(b) módulo , apontando de pra
(c) módulo , apontando de pra
(d) módulo , apontando de pra
(e) módulo , apontando de pra
Passo 1
Num movimento circular, tem a aceleração tangencial, tangente ao movimento, e a aceleração centrípeta, que aponta pro meio da trajetória.
Mas o movimento é circular uniforme! Isso significa que o módulo da velocidade da partícula não varia, então a partícula não tem aceleração tangencial. Portanto, a sua aceleração é só centrípeta.
Ou seja, o vetor aceleração da partícula aponta de pra .
Show, só assim de bobeira já eliminamos 3 alternativas!
Passo 2
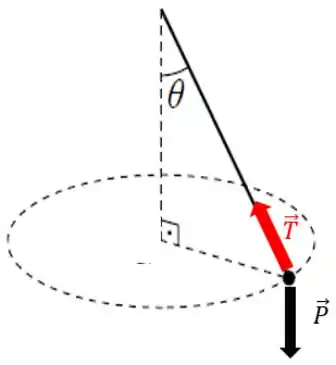
E já que estamos falando de aceleração, por que não usar a 2ª lei de Newton? As únicas forças atuando na partícula são seu peso e a tração no fio :
Passo 3
Mas já que a aceleração é só centrípeta, a boa é decompor essas forças pra elas terem uma componente centrípeta. No caso a não dá pra decompor porque ela já é perpendicular à direção centrípeta, mas a dá!
Vou considerar esse triângulo que tá aparecendo aí na figura de cima. Aplicando uma trigonometria básica, a decomposição da força vai ser:
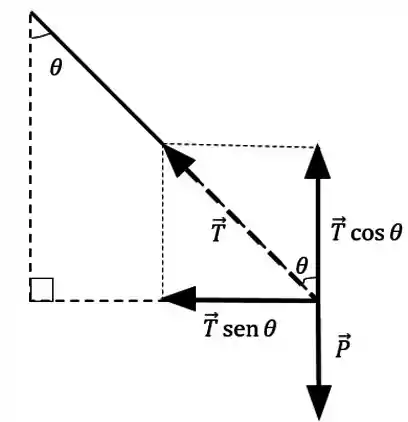
Passo 4
A força resultante na direção centrípeta é , então, pela 2ª lei de Newton:
Mas já vimos que a aceleração total da partícula é igual à sua aceleração centrípeta, então podemos trocar por , o que dá:
Então pra achar , precisamos do valor de !
Passo 5
A partícula não tem movimento no sentido vertical, então as forças e se cancelam:
E , então:
Passo 6
Show! Então vamos ter:
Resposta
Alternativa (d)