Um disco horizontal, com um raio de roda em torno de um eixo vertical que passa pelo seu centro. O disco parte do repouso em e tem uma aceleração angular constante de . Em que instante de tempo as componentes radial e tangencial da aceleração linear de um ponto sobre a borda do disco serão iguais em magnitude?
a)
b)
c)
d)
e)
Passo 1
O problema quer saber o instante de tempo em que a aceleração tangencial terá o mesmo módulo que a aceleração centrípeta.
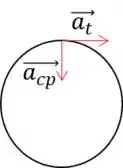
Para a aceleração tangencial podemos utilizar:
Já para a aceleração centrípeta podemos utilizar:
Entretanto não é interessante termos velocidade na nossa equação, vamos tentar substituir ela por outra coisa. Podemos utilizar:
Como o disco parte do repouso, a velocidade inicial é nula. Restando apenas:
Substituindo:
Substituindo :
Como a aceleração centrípeta precisa ter o mesmo módulo que a aceleração tangencial, fazemos:
Substituindo a aceleração angular:
Resposta
Alternativa