Para o pêndulo cônico ao lado, e a massa é .
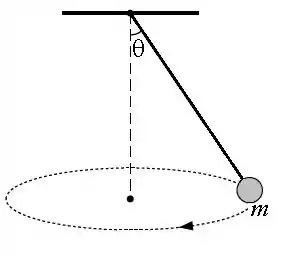
(a) Anote na figura as forças que agem no pêndulo.
(b) Escreva as equações que governam o movimento do pêndulo. Utilize um sistema de coordenadas em que um dos eixos aponte na direção do centro da trajetória.
(c) Determine o módulo da força resultante que atua no pêndulo.
Passo 1
Estabelecer um sistema de coordenadas
Antes de mais nada, vamos primeiro dar nome aos bois. Ou melhor, aos eixos. Usando o Sistema Cartesiano de Coordenadas, com a origem posicionada no centro da bolinha, estabelecemos nossos eixos , e .
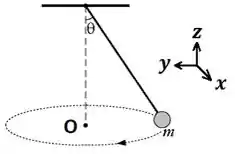
Passo 2
Identificar forças atuando no sistema
Para analisar as forças que atuam na bolinha, vamos primeiro lembrar o que está acontecendo, beleza? Primeiramente, como a bola não está no espaço sideral nem nada e sim no nosso querido planeta, vamos ter uma força peso atuando sobre ela. A força peso “apontará” pra baixo e terá o módulo igual à:
Mas só essa força? Jura? Er...não. Até porque, a bola não estaria rodando se não houvesse a corda, não é mesmo? Se, por algum motivo doido, a gente quisesse estragar o pêndulo e cortasse a corda, a bola iria cair!
Se a bolinha não cai, é porque a corda exerce uma força sobre ela no sentido contrário! Essa força vai ser então a famosa Tensão da Corda (). Representamos então as forças que atuam sobre a bolinha por:
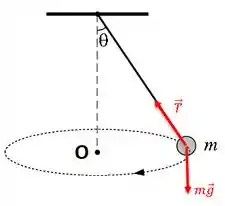
Passo 3
(b) Analisar as componentes da tensão da corda
Lembra que a tensão da corda está angulada em relação ao eixo de coordenadas? Pois bem, pra gente escrever as equações que governam o movimento do pêndulo temos que analisar as componentes da tensão. A gente vai fazer isso pra poder ver o que acontece isoladamente na vertical e na horizontal, beleza? Vamos lá então:
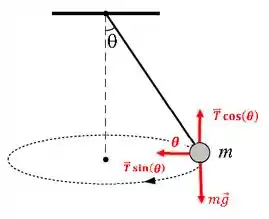
Na horizontal, a única força que atua é a componente e ela vai atuar como força centrípeta. Porque? Bem, se ela não fizesse isso o pêndulo não estaria girando! Então vamos ter:
Na vertical já vamos ter duas forças. O enunciado não falou nada de o pêndulo estar girando enquanto cai ou sobe não é mesmo? Então podemos igualar as duas forças na vertical:
Passo 4
(c) Partir pras contas
No passo anterior vimos que a resultante das forças na vertical era nula, não é mesmo? Então a resultante de todas as forças vai ser a força na horizontal:
Mas das forças na vertical, temos a seguinte relação:
Se substituirmos em , vamos ficar com:
E ai agora é só substituir os valores! Partiu então:
Resposta
- Forças e