Um bloco 1 de massa é lançado de uma altura vertical ao longo de uma rampa e colide frontalmente com o bloco 2 de massa , que se encontrava em repouso na horizontal (veja a figura). Após a colisão, o bloco 1 retorna para a esquerda enquanto o bloco 2 sai para a direita, ambos com o mesmo módulo de velocidade, . O bloco 2 seguirá a trajetória entrando na pista semi-circular. Não há atrito dos blocos com o piso durante todo o percurso.
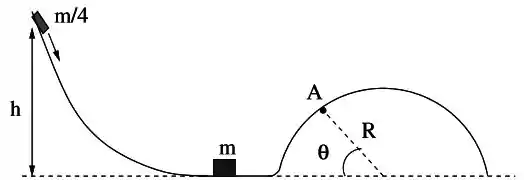
As respostas devem ser dadas em função dos dados que constam no desenho e/ou no texto acima, a saber: , , , e .
a) Ache a altura vertical máxima que o bloco 1 alcança após a colisão.
b) Ache a velocidade do bloco 1, , logo antes da colisão. Com isto, ache a velocidade original com que foi lançado, , quando partiu da altura .
c) Ache a velocidade com que o bloco 2 alcança o ponto , a um ângulo como mostrado na figura.
d) Ache o módulo da força normal sobre o bloco 2 em .
Passo 1
(a)
Conhecemos a velocidade do bloco 1 após a colisão: . Por conservação de energia mecânica, a altura alcançada após a colisão é dada por:
Passo 2
(b)
Por conservação de momento linear na colisão temos:
Sendo:
Logo, substituindo todos os dados:
Esta é a velocidade do bloco 1 antes da colisão, portanto após a descida. Para encontrar a velocidade inicial quando estava a uma altura , usamos conservação de energia mecânica:
Passo 3
(c)
Aqui novamente usamos conservação de energia mecânica. O bloco 2, após subir uma altura:
Terá velocidade dada por:
Passo 4
(d)
No ponto atuam sobre o bloco 2 a normal e o peso.
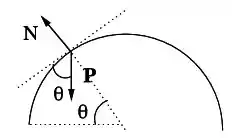
De acordo ao diagrama de forças, vemos que a força resultante na direção centrípeta está dada por:
Portanto:
Substituindo obtido no item anterior, obtemos:
Podemos separar a fração:
Resposta
(a)
(b) ;
(c)
(d)