Em uma competição de uma olimpíada de inverno um esquiador de massa deve descer uma pista de neve em formato de de círculo de raio , como ilustrado ao lado. Sabendo que ele parte do repouso e que a razão entre o quadrado da sua velocidade e a altura é igual ao dobro da aceleração da gravidade , responda os itens abaixo em função de , e . Considere o atrito desprezível.
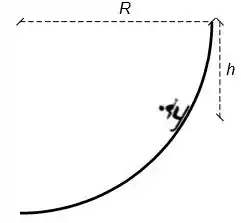
a) Faça um diagrama de corpo livre representando as forças que agem no esquiador, quando ele está à meia altura da pista.
b) Nesta posição, calcule o módulo da velocidade do esquiador e direção que ela faz com eixo vertical.
c) Ainda nesta posição, calcule o módulo da aceleração resultante.
d) Agora o esquiador chega no final da pista. Calcule nesta posição a força normal que a neve faz sobre ele.
Passo 1
a)
As únicas forças que atuam sobre o esquiador é a força normal perpendicular à superfície e a força peso que sempre aponta para baixo.
Além disso, como o problema nos diz que o esquiador está a meia altura, então . Com isso podemos montar também um triângulo retângulo para descobrir a angulação através de relação trigonométrica.
Agora podemos fazer um desenho completo:
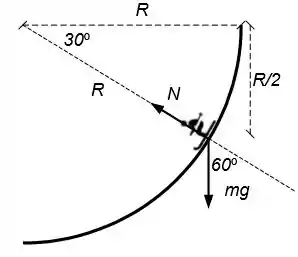
Passo 2
b)
O problema nos disse que: “a razão entre o quadrado da sua velocidade e a altura é igual ao dobro da aceleração da gravidade ”. Escrevendo isso matematicamente, temos:
A velocidade do esquiador é sempre tangente a trajetória. Como queremos saber o ângulo que ela faz com a vertical e já temos a força peso como referência de vertical, basta saber o ângulo que a velocidade faz com a força peso. Pela figura, vemos que esse ângulo é justamente .
Portanto, a velocidade faz um ângulo de com a direção vertical.
Passo 3
c)
Temos duas acelerações, a centrípeta e a tangencial. Vamos calcular elas primeiro para depois calcular a aceleração resultante.
A aceleração centrípeta tem a fórmula:
Substituindo os dados:
Agora a aceleração tangencial é justamente a parcela da gravidade que influencia no movimento do esquiador. Ou seja:
Agora é só usar a fórmula do módulo de um vetor para encontrar o módulo da aceleração resultante:
Passo 4
d)
Usando novamente o enunciado: “a razão entre o quadrado da sua velocidade e a altura é igual ao dobro da aceleração da gravidade ”. Só que agora a altura vale .
Aplicando a segunda lei de Newton na vertical, sabemos que a aceleração produzida tem que ser a aceleração centrípeta:
Substituindo o que encontramos:
Resposta
a)
b) ; Ela faz um ângulo de com a direção vertical.
c)
d)