Uma esfera muito pequena de massa está amarrada a uma haste vertical giratória por dois fios ideiais de comprimento . A haste gira de modo que os fios fiquem tensos formando com a haste um triângulo que mantem seu formato inalterado durante o movimento, conforme ilustra a figura. Sabendo que os fios de cima e de baixo fazem o mesmo ângulo com a horizontal e que a velocidade de rotação da esfera tem módulo constante , determine
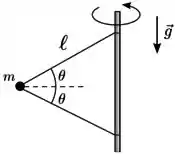
- O módulo e a orientação (direção e sentido) da força resultante sobre a esfera;
- O módulo da tensão no fio superior e o módulo da tensão no fio inferior;
- O limite mínimo do módulo da velocidade de rotação da esfera em torno da haste para que o fio inferior se mantenha esticado.
Passo 1
Vamso começar escrevendo os dados do enunciado
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
Como a esfera não está subindo nem descendo, ela só vai ter força resultante no sentido do centro da rotação, já que ela está girando.
Que força vai ser essa? A força centrípeta
Mas repara que não temos o raio de rotação, vamos dar uma olhada na geometria desse desenho
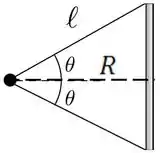
Podemos “decompor” par achar , usando a “regra do COlado, SEparado”.
Vamos ter ali na fórmula da força centrípeta
Passo 3
b)
Para descobrirmos as forças devemos fazer o DCL da esfera
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Não, ele não está em contanto com nenhuma superfície.
Sim, temos dois fios atuando.
Não, não existe mola atuando.
Não, não existe atrito.
O DCL fica
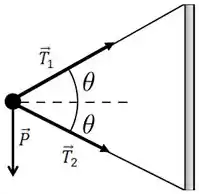
Passo 4
Vasmo fazer agora a análise das forças no , isso porque ele está em equilíbrio. Não vai fazer muita diferença porque vamos precisar fazer nos dois eixos
Devemos encontrar usando a “regra do COlado, SEparado”.
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 5
Vamos agora fazer no , lembrando que a força resultante é a força centrípeta que encontramos ali em cima
Devemos encontrar usando a “regra do COlado, SEparado”.
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 6
Vasmo escrever as duas equações que temos
Podemos somar as duas equações
Passo 7
Podemos agora, multiplicar a primeira equação por
Fiz isso porque ao somar, dessa vez, sobre apenas
Passo 8
c)
Para o fio ficar esticado, a força nele deve ser pelo menos zero. Isso nos diz que a situação limite é