A figura abaixo mostra um sistema composto por duas partículas, ambas com massa , conectadas por fios inextensíveis e de massas desprezíveis de comprimento cada.
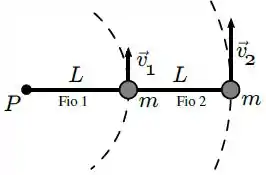
O fio está preso ao ponto fixo , enquanto o fio liga uma partícula à outra. O sistema gira em torno do ponto sobre uma superfície plana horizontal sem atrito, com velocidade angular .
Os módulos das velocidades e de cada partícula são constantes. e são as trações nos fios e respectivamente. Marque a alternativa correta:
Passo 1
Não se deixe perder pela quantidade de informações no enunciado. Vamos um passo de cada vez.
A primeira partícula está girando ao redor do ponto com o módulo da velocidade constante. Ela está descrevendo um movimento circular uniforme.
Neste caso, temos que ter uma força centrípeta que a obrigue a descrever essa circunferência.
As forças que atuam nela são as trações dos dois cabos, que estão sempre na direção do raio da circunferência!
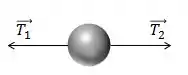
A força resultante vai também ser na direção do raio, tendo que ser a força centrípeta!
Em módulo, temos:
Mas a força centrípeta tem uma fórmula própria pra ela!
A massa da partícula é e o raio da circunferência é . Para achar a velocidade , usamos a velocidade angular . Para passar de uma para a outra, fazemos:
Temos então . Substituindo tudo:
Assim:
Passo 2
Vejamos a partícula . A única força que vai atuar nela é a tração do segundo fio.
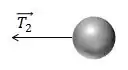
E vai valer a mesma discussão anterior, sendo a força centrípeta nessa partícula igual à tração no fio .
Que em módulo fica:
Usando a fórmula da aceleração centrípeta:
Dessa vez, é o raio da circunferência descrita pela segunda partícula, e . A velocidade linear também vai mudar, pois a velocidade angular das duas partículas é a mesma e o raio mudou.
Temos .
Substituindo na equação que tínhamos antes:
A resposta então é a letra (d).
Resposta
Letra (d)