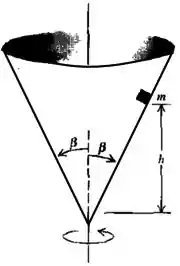
Um pequeno bloco de massa é colocado no interior de um cone invertido que gira em torno do eixo vertical. As paredes do cone fazem um ângulo com a vertical. O coeficiente de atrito estático entre o bloco e o cone é . Para que o bloco permaneça a uma altura acima do vértice do cone, qual deve ser o valor mínimo de ?
Passo 1
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
O DCL do bloco fica
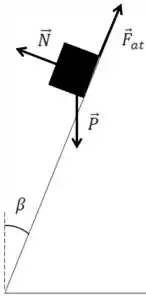
Nesse caso, por mais que estejamos em um plano inclinado, como ele está rodando é importante determinarmos a resultante na direção do centro da curva. E como ele pretende que ele não caia é melhor, neste caso, usarmos os em relação ao chão e não em relação a superfície inclinada.
Está mega confuso essas forças né? Vamos tentar ver em um esquema melhor
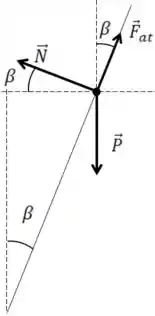
Como fizemos essa mudança de ângulo? Precisamos lembrar um pouco sobre geometria. Vamos entender melhor isso
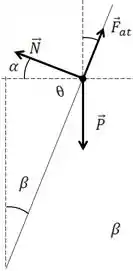
Repara que
Além disso
Então
Além disso, o ângulo do com a é um ângulo entre retas paralelas. Também sendo .
Voltando à física.
Passo 2
Vamos fazer o equilíbrio no
Vamos começar encontrando a componente da , usando a “regra do COlado, SEparado”.
Passo 3
Vamos agora achar a componente da , usando a “regra do COlado, SEparado”.
Teremos então
Passo 4
Vamos agora ao
Sabemos que o módulo da força centrípeta deve ser igual ao módulo na componente da normal menos a componente da .
Vamos primeiro achar o módulo de
Passo 5
Para o módulo da força centrípeta, devemos saber o raio do movimento também, já que a velocidade é algo que queremos descobrir.
O raio pode ser resolvido olhando para essa figura e usando trigonometria.
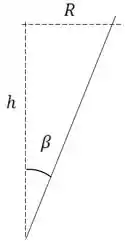
Passo 6
Para a componente da força de atrito, temos:
Teremos então