Você gira uma bola em círculos em um plano vertical, usando uma corda de comprimento . Existe uma velocidade angular mínima que você deve manter para que a bola execute o círculo completo. Se você girar a bola com velocidade angular menor do que , a corda fica frouxa e a bola não consegue chegar ao ponto mais alto do círculo. Qual o valor de em rpm?
Dados:
(A) rpm
(B) rpm
(C) rpm
(D) rpm
(E) rpm
Passo 1
A situação é a seguinte. A gente está girando a bolinha em azul na vertical:
Se a bolinha está realizando um movimento circular, existe uma força centrípeta associada a esse movimento.
Mas quais forças que estão atuando sobre a bolinha?
Ao longo de todo o movimento, há uma força peso apontando para baixo e uma força de tração puxando no sentido da corda:

Entretanto, se queremos achar a velocidade angular mínima com que a bolinha consegue realizar esse movimento. Isso significa que a bola está quaaaaase afrouxando a corda, ou seja, a força de tração é nula nesse ponto mais alto:
Sobra apenas a força peso :
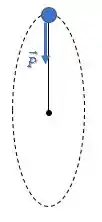
Assim, ela será a única força atuando como força centrípeta.
Podemos igualar com a expressão dessa força:
Passo 2
Porém, como queremos achar em função da velocidade angular e não da velocidade linear, podemos utilizar a relação:
Substituindo isso, temos:
Passo 3
Então, no ponto mais alto, a velocidade angular mínima será:
Substituindo os valores, temos
Assim, a velocidade angular mínima para que a bola realize o movimento é aproximadamente:
Mas queremos na unidade de rpm (rotações por minuto).
Passo 4
A unidade de radianos por segundo ) mostra um deslocamento angular por segundo, ou seja, se cada volta tem , podemos dividir por esse valor que teremos o número de rotações por segundo:
Como queremos o número de rotações por minuto, basta multiplicar esse número por :
Ficamos com a letra (A).
Resposta
Letra (A)