Calcule
Onde
Passo 1
Oi, tudo bem?
O problema nos pediu para calcularmos essa integral dupla:

Precisamos fazer um esboço dessa região!
Observando os extremos dos intervalos temos essas três equações:
Assim a região de interesse é a região compreendida por essas três equações:
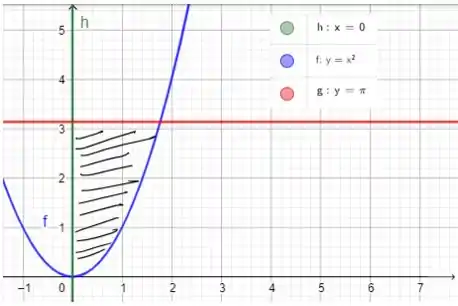
Então temos que usar esses limites para construir nossa integral:
E usar a ordem de integração correta!

Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos dar uma olhada com mais carinho nos nossos limites de integração em :
Mas como integrar? Vamos sempre começar pela variável que tiver os extremos do intervalo com funções, deixando para o final a variável que tem limites finitos. No nosso caso seria , assim ao integrarmos em aplicarmos os limites de integração, vamos ter um resultado apenas em .
Beleza até aqui? E quais os limites em ? Vamos resgatar a figura lá do passo 1:
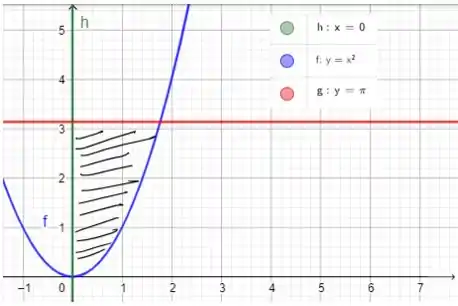
Como vemos o limite mais à esquerda é , mas e o mais à direita? É quando as curvas azul e vermelha se encontram, ou seja
Sendo assim o intervalo de é
Aí a ideia é começar integrando em , aplicar os limites. Depois com uma integral apenas em , é só integrar e aplicar nos limites (que vão ser números) e deu!

Aí nosso fica nessa ordem:
Com esses limites de integração:
Agora #partiu montar a integral dupla:
Obs.: a escolha ou influencia nos limites de integração, mas não muda o resultado viu! Escolhi dessa forma por simplicidade, mas você pode fazer o exercício de inverter e comparar os resultados! Eles precisam ser iguaizinhos!
Tudo bem até aqui?
Bora integrar essa coisa?
Passo 3
Agora vamos integrar essa coisa:
Integrando em , vamos considerar constante (e pode até sair da integral mais de dentro), daí temos:
Aplicando os limites vamos ter um resultado apenas em :

Passo 4
Nossa missão agora é terminar de calcular a integral. Note que temos agora uma integral apenas em x!
Usando a técnica de integração por partes usando e temos o seguinte:
E retornando para :

Ufa! Agora sim! Terminamos! Espero ter ajudado!
Até próxima!