USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 29b
Calcule a massa da região R limitada por:
com .
Passo 1
Olá meu amigo, pronto para calcular uma massa de uma região por meio de integrais? Não? Poxa mas voce vai ter que fazer pois é isso que a questão nos propõe.
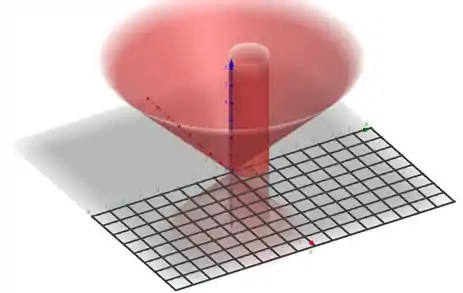
A região de integração é a região do cone e do nosso tubo que coincide com a ranhura preta.
Passo 2
Vamos pensar agora na nossa parametrização,
E o nosso jacobiano é
Agora que nós temos nossa parametrização, vamos descobrir os nossos limites de integração
Como estamos no primeiro quadrante
Passo 3
Agora é hora de calcularmos de fato a nossa integral
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x