USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 29c
Calcule a massa da região R limitada por:
c) , com
Passo 1
Olá meu nobre colega, hoje iremos botar a mão na massa para calcular a massa da região R abaixo,
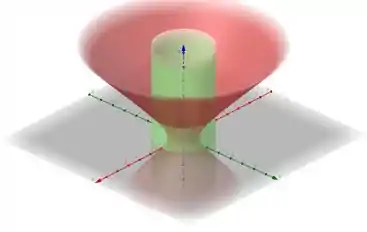
A piadoca foi péssima, mas prometo que a resolução da questão será melhor. Primeira coisa que iremos fazer é parametrizar tudo, pois assim teremos nossa vida facilitada,
O nosso querido jacobiano é
Então agora nos resta encontrar os limites de integração para a parametrização usada,
Passo 2
Passando agora para a parte de montar nossa integral tripla e resolve-la
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x