USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 29e
Calcule a massa da região R limitada por:
e) , com ;
Passo 1
Olá meu caro amigo, hoje iremos calcular a massa de uma região no mínimo interessante. Vamos dar uma olhada nela para eu lhe explicar.
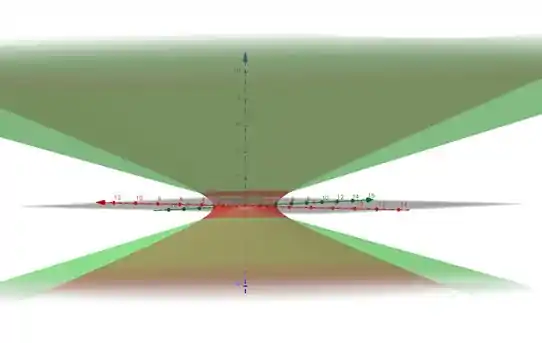
Então nossa região é essa acima, veja que temos os pontos para . E veja também que a nossa região vai até quando a parte verde ‘fura’ a parte vermelha. Agora iremos parametrizar a nossa região
E o nosso jacobiano
Passo 2
Agora iremos encontrar os limites de integração a partir da parametrização que fizemos,
Os limites de z
Passo 3
Agora iremos montar a nossa integral e calcular a massa
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x