USP, Sem Campus, Cálculo 3, Lista 1 - 2023.1, Questão 5g
Calcule as seguintes integrais duplas:
g)
Onde .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a seguinte integral dupla:
Onde .
Perceba que a região de integração é a região interna ao círculo de raio , veja:
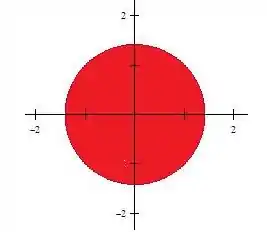
Nós podemos utilizar a simetria do sistema para resolver a nossa integral!!
Eaí? Bora lá resolver?
😉
Passo 2
Bom... observe que, como a tangente é uma função ímpar, é uma função ímpar de variável .
Assim, a parte da integral que envolve essa função será nula, pois o intervalo de integração é simétrico em . Portanto:
De forma análoga, temos também que:
Com base nisso, a gente pode concluir que:
Agora vamos resolver a integral que nos restou!!
Passo 3
Agora, resolvendo a integral dupla que restou, temos:
A integral dupla é nada mais do que a área do círculo, logo:
Entendeu direitinho? Responde aee ;)
