UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 2
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
2 - , a região do primeiro quadrante dada por
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema, queremos obter a integral da função aplicada na região , onde é a região definida entre e no primeiro quadrante do plano .
E aí, tem ideia do que fazer? 🤔
O segredo é conseguir definir a região como os limites de integração de
Se conseguirmos fazer isso, a primeira integral deve ser definida entre duas funções e a última integral deve ser definida entre duas constantes.
Bora começar! 😁
Passo 2
Vamos começar esboçando a região .
A inequação nos dá um círculo de raio como podemos perceber da estrutura da equação e nos diz que varia de até .
Plotando essas informações no plano , temos
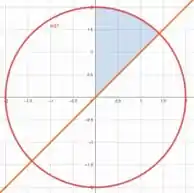
Como nossa região tem características circulares, podemos usar coordenadas polares para nos ajudar na integral.
Para converter as coordenadas , e para as coordenadas polares temos que substituir por , por e integrar com relação a e a .
Já vimos que varia de a e é o ângulo que a região varia com o semieixo positivo de , no caso, de a .
Entendeu essa parte? 😎
Passo 3
Montando nossa integral em coordenadas polares sem esquecer do jacobiano , vamos obter
Integrando com relação a , temos
Aplicando os limites de integração de
Integrando o resultado em função de
Aplicando os limites de integração de
Sacou como faz? Responde Aí! 😉
