Use integral dupla para calcular a área da região limitada por:
Passo 1
Pois bem! Em problemas como esse devemos sempre começar fazendo um esboço da região. Mas não se preocupe, pois fazer isso significa colocar no plano todas as curvas dadas. Vamos começar aqui colocando as mais simples primeiro: , e .
A primeira, , nada mais é do que uma reta, afinal de contas
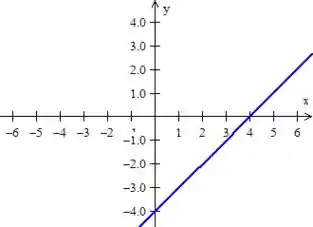
Quanto a segunda, , e a terceira , são duas retas também, mas são retas paralelas ao
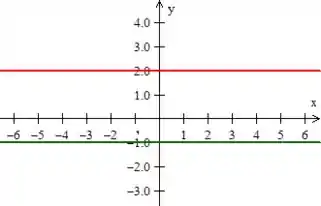
Bem...! Em relação à última equação , estamos falando de uma parábola
Mas cuidado! Pois essa parábola é uma parábola ao redor de e não em como estamos acostumados. Além disso, como é negativo, sua concavidade é para a esquerda:
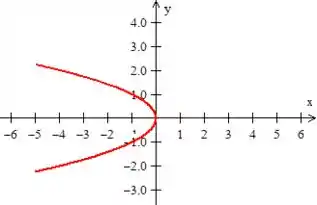
O legal é que já dá pra ver que região (chamaremos de ) estamos trabalhando! :D
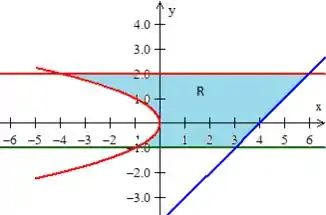
Agora temos que descrever essa região, e vamos fazer isso descrevendo em uma região do tipo .
Passo 2
Nesse tipo de região, devemos ter que varia em um intervalo numérico bem definido.
O que nessa região é bem easy verificar apenas observando a imagem que
Passo 3
Bem...! Quanto à variação do dentro dessa região, ele entra na equação na curva vermelha...
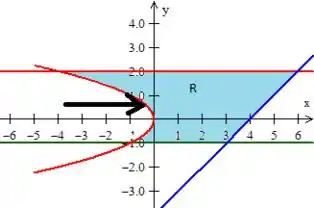
e sai na reta azul
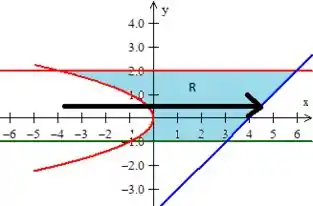
Ou seja
Passo 4
Como você já deve saber, área de uma região a essa altura do campeonato é:
como a região acabamos de descrevê-la
Podemos simplesmente substituir na integral dupla (mas não se esqueça que o limite numérico sempre vem primeiro ):
Bora resolver essa integral aí?
Passo 5
Primeiro calculemos a integral de dentro...
Substituindo os limites de integração em ...
Calculando essa integral...
substituindo os limites encontramos...