Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 156123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

a Para começar, vamos procurar as interseções dessas funções aí. Igualando elas nós temos:

x 3 2 = 2 x → x 3 2 - 2 x = 0

x x 1 2 - 2 = 0

Esse caso aí vai ter duas soluções:

x = 0       ;       x 1 2 - 2 = 0 → x 1 2 = 2

x = 0           ;           x = 4

Ok, os gráficos serão dois polinômios que se cruzam em x = 0 e x = 4 . Entre esses valores de x , o gráfico que fica por cima é o y = 2 x . Para confirmar isso, basta substituir um valor de x entre as interseções e ver quem é maior. Para x = 1 por exemplo:

y 1 = 2 1 = 2           ;           y 1 = 1 3 2 = 1

Esboçando R sendo a região entre os gráficos, teremos a reta y = 2 x e a curva y = x 3 2 :

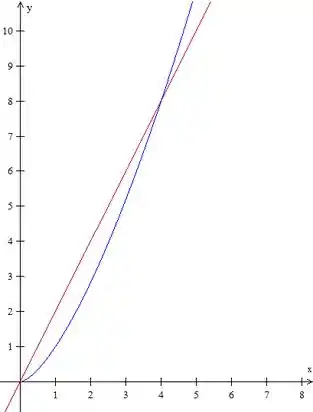
Passo 2

Para calcular a sua área, fazemos a integral da diferença entre os gráficos, de x = 0 até x = 4 :

A = ∫ 0 4 2 x - x 3 2 d x

= x 2 - x 5 2 5 2 [ 4 0 = 4 2 - 2 4 5 2 5 - 0 2 - 2 0 5 2 5

= 16 - 64 5 = 16 5   u . a .

Passo 3

b Vamos ter que calcular agora o volume gerado pela rotação dessa região em torno do eixo x . Para isso, faremos a diferença entre os volumes gerados por uma e por outra rotação. Na integral, o volume maior seria gerado pela função mais afastada do eixo, no caso será a y = 2 x , e o volume menos pela outra função y = x 3 2 , que é mais interna:

V = ∫ 0 4 π 2 x 2 - x 3 2 2 d x = ∫ 0 4 π 4 x 2 - x 3 d x

= π 4 x 3 3 - x 4 4 [ 4 0 = π 4 4 3 3 - 4 4 4 - π 4 0 3 3 - 0 4 4

= π 256 3 - 256 4 - π 0 = π 256 12 = 64 π 3   u . v .

Resposta

a   A = 16 5   u . a .

b   V = 64 π 3   u . v .

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .