USP – Sem Campus – Cálculo 2 – Provas Antigas – P2 – N3 – 2021.2 – Questão 1
Calcule o volume do sólido gerado pela rotação da região delimitada pelos gráficos de e e pelas retas verticais e , girando em torno da reta .
Resposta:
Passo 1
Eaew, tudo certinho com você?
O enunciado nos traz uma região que é delimitada pelo gráfico de duas funções, , que é uma parábola, e uma reta dada por . O enunciado também coloca retas verticais que delimitam nossa região, estas são e , e precisamos calcular o volume do sólido de revolução quando esta região é revolucionada (rotacionada) ao redor de . A primeira coisa é dar uma olhada em nossa região, temos o seguinte
É o pedacinho mais escuro entre as linhas pontilhadas em azul. No topo, temos em roxo a nossa reta horizontal . Ao rotacionar em torno da reta horizontal, vamos obter um sólido que tem um buraquinho no meio, onde a parede interna é dada pela parábola e a parede exterior é dada pela reta. O nosso sólido tem a seguinte forma
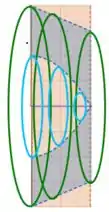
O segredo é calcular o volume deste sólido como se não houvesse buraco, e, então, remover o volume do buraco! Vamos tentar fazer isso!
Passo 2
Primeiro, vamos considerar que o volume é completo, temos que ao fatiar esta figura sem buraco, obtemos discos de raio dado pela equação da reta, mas deslocado acima da origem em nosso referencial. Podemos calcular o volume utilizando
Se a revolução fosse em torno de , teríamos que o raio seria dado por , ou seja
Mas, na verdade, temos que a revolução ocorre em , portanto, devemos subtrair que está excedente em nosso referencial, de forma que nosso raio é
Vamos aplicar a nossa integral e calcular este volume!
Passo 3
Temos que o volume completo é obtido substituindo a equação (2) na equação (1), temos que
Expandindo o quadrado, temos que . Voltando em nossa integral
Vamos ter que separar em três integrais e identificar nossas primitivas, belezinha?
Passo 4
A nossa equação (3) tem a forma
Usando que
Ou seja, o volume completo é tal que
Avaliando os limites de integração, temos
Ou seja, temos que
Ainda precisamos subtrair o volume do buraco! Vamos lá!
Passo 5
Da mesma forma que anteriormente, o volume é calculado como
Mas agora o raio é dado pela equação da parábola , mas novamente, precisamos considerar que há um excedente em nossa escolha de referencial, ou seja, nosso raio é tal que
E o nosso volume toma a forma
Vamos resolver esta equação, belezinha?
Passo 6
Expandindo o quadrado, temos , ou seja
Que pode ser separado em três integrais
Utilizando novamente a equação (4) temos que
E, avaliando os limites, temos
Resumindo, temos que
Estamos quase lá! Agora é só calcular!
Passo 7
Temos então que nosso volume é
Precisamos fazer o MMC, para calcular esta diferença
Dividindo em cima em baixo por 9, temos
A questão é isso, te vejo na próxima! Tchauzinho!