Considera a região
Determine o volume do sólido obtido pela rotação da região em torno da reta .
Passo 1
Olha eu sinceramente não faço ideia de como é o gráfico desse mas eu posso substituir os limites de integração e fazer a seguinte análise:
Essa derivada, quando olhamos para um intervalo entre e (que é o caso do intervalo ), é positiva, o que significa que o gráfico cresce. Sabendo que e , sabemos que o gráfico será algo similar a isso aqui embaixo (para achar o gráfico de basta fazer a mesma coisa só que espelhado em relação ao eixo ):
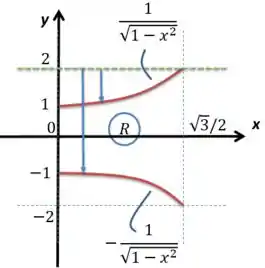
Essa é a do problema! Girar em torno de , como pedido na questão, seria girar em torno da horizontal que passa no dp eixo , seria esse eixo verde aí. Repara que o vai gerar um sólido de raio menor que o , sendo o primeiro raio igual a e o segundo igual a , representados pelas setas azuis. Logo, a integral é a diferença da rotação desse segundo raio pela rotação do primeiro raio:
Só resolver essa coisa feia aí em cima!
Ok, você pode até não lembrar, mas a integral de é . Aí fica mole, saca: