Considere a seguinte região do plano: . O volume do sólido obtido pela rotação de A em torno da reta horizontal é igual a:

Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Primeiro, temos que interpretar o que é essa região do plano A para depois rotacionarmos esse plano que a questão pede pra gente calcular. Essa região é dada pela intersecção de duas funções que a questão define pra gente como:

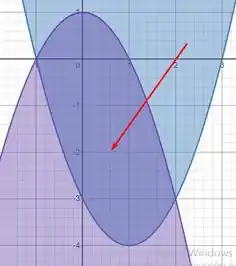
Podemos notar que no gráfico elas se interceptam em dois pontos. Para acharmos esses pontos, basta igualarmos as funções. Logo,

Logo, as raízes para esse polinômio são e . E esses são justamente os limites de integração para calcularmos o volume do sólido de revolução da área.