UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 6b
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo :
A região do primeiro quadrante limitada superiormente pela parábola , inferiormente pelo eixo e à direita pela reta .
Passo 1
E aí genteeee, tudo tranquilo por aí? Vamos matar mais uma questãozinha de cálculo junto comigo!!
Nessa questão, temos uma região no quadrante do plano que é limitada pelas curvas:
Quando rotacionamos essa região em torno do eixo formamos um sólido. Precisamos determinar o volume desse sólido de revolução, beleza?
Masss, como que calculamos volume de sólido de revolução mesmoo? Alguém tá lembrado de um dos métodos??
Bom, como estamos falando de rotação em torno do eixo , um método que facilita um pouco o trabalho algébrico é o método das cascas. Segundo ele:
Massa! Então, eis aqui o que vamos fazer pra matar essa questão:
- Identificar a região que está sendo rotacionada;
- Montar a integral do volume seguindo o método das cascas;
- Resolver a integral e encontrar o tão esperado volume.
Show?! Vamo nessa!
Passo 2
Devemos começar identificando a região que será rotacionada. Para isso, vamos analisar curva a curva:
A primeira curva é a parábola , ela possui vértice em e pelo enunciado, estamos interessados apenas no quadrante (região em que ). Logo:
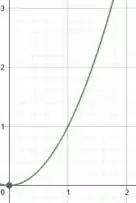
As outras duas curvas são retas constantes, uma delas é o próprio eixo e a outra é a reta , uma reta vertical passando por (claro né, haha). Assim, colocando tudo em um mesmo gráfico:
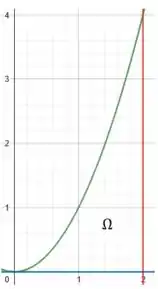
Boaaaa! Então, conseguimos visualizar a nossa região . Agora vamos pensar nas integrais!!
Passo 3
Bom, o nosso querido método das cascas calcula o volume obtido pela rotação da região abaixo da nossa curva , pra um dado intervalo de valores em .
Analisando a nossa região rotacionada :
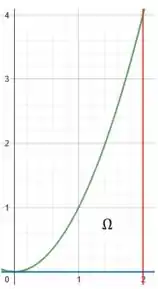
Vemos que ela é justamente a região abaixo da curva no intervalo de a . ]
Lembrando que, por esse método:
Teremos:
Pra calcular essa integral, vamos começar colocando as constantes para fora:
Logo:
Por fim:
Prontinho galera. Conseguiram entender? Responde Aí!