UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 5f
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
f)
Passo 1
Opaaa pessoal, tudo bom com vocês?
Nesse exercício, basicamente temos uma região no plano e vamos rotacioná-la em torno do eixo . Após efetuar a rotação, teremos um sólido. O enunciado nos pede pra determinar o volume desse sólido, beleza?
Antes de tudo, precisaremos analisar qual a região que será rotacionada. Segundo o enunciado, ela está limitada pelas curvas:
Ok! Depois de identificarmos a região precisaremos calcular, efetivamente, o volume desse sólido de revolução. Vocês lembram como podemos fazer isso?
Temos que usar algum dos nossos métodos para cálculo de sólido revolução. Um que pode ser interessante é o método dos discos, segundo ele:
Show de bola! Então vamos lá 😊
Passo 2
Pra começar, vamos identificar a nossa região do plano que será rotacionada. Como falamos no passo , ela é limitada por curvas:
As duas primeiras curvas são funções trigonométricas, nas quais as curvas possuem o seguinte formato:
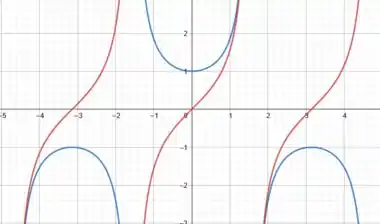
onde a curva azul é e a curva vermelha é .
As nossas duas últimas curvas são retas verticais constantes, é o próprio eixo e é uma reta vertical que passa pelo ponto .
Assim, adicionando todas as curvas no gráfico, temos:
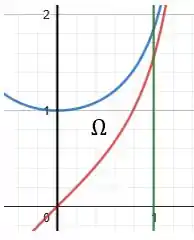
Prontinho, essa região do meio é a região , que será rotacionada em torno do eixo .
Passo 3
Agora vamos montar as integrais.
Antes de começarmos, é importante entender que no método dos discos, pra calcular o volume obtido pela rotação de uma região abaixo da curva , usamos:
Assim, para calcularmos o volume obtido pela rotação de por esse método, precisamos fazer uma operação entre volumes. Podemos dizer que:
onde:
é o volume obtido pela rotação da região abaixo de no intervalo em que se encontra.
é o volume obtido pela rotação da região abaixo de no intervalo em que se encontra.
E pra que servem as retas e ?
É justamente pra determinar nossos limites de integração: .
Pegaram a ideia?
Assim, podemos montar as nossas integrais pelo método dos discos.
Lembrando que:
Temos:
E:
Perfeito!
Passo 4
Pra finalizar, vamos calcular as nossas integrais.
Colocando pra fora da integral:
Mas, lembram qual é a derivada da tangente?
Logo, pelo teorema fundamental do cálculo:
Como :
Vamos agora para :
Tem uma relação trigonométrica bem legal que podemos usar aqui, e que vai nos poupar um trabalhinho algébrico...
Da relação fundamental da trigonometria, sabemos que:
Dividindo ambos os lados por chegamos que:
Substituindo esse resultado dentro do integrando de , vem:
O primeiro termo da equação acima é justamente o volume , que calculamos anteriormente. Ou seja:
Já o segundo termo, vale:
Ou seja:
Agora é só substituir na relação que escrevemos para e correr pro abraço:
Então: