A região destacada na figura abaixo é delimitada pelas funções e .
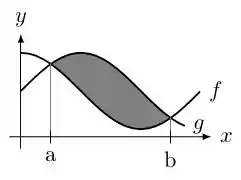
Sabemos que
O volume do sólido de revolução obtido girando em torno do eixo é:
- .
- .
- .
- .
Passo 1
Vamos primeiro ver qual técnica para encontrar o volume iremos usar. Temos que a região está girando em torno do eixo , então deve ser interessante usar o método dos discos cilíndricos.
De maneira geral, a fórmula do volume será:
é o intervalo de integração. Como está limitada pelas interseções e , então:
Da mesma forma, vemos que a curva superior é e a inferior é . Ou seja:
Vamos tentar chegar nessa integral a partir dos valores dados.
Passo 2
Primeiramente, vamos separar a integral usando a propriedade da subtração de integrais:
A integral da esquerda é bem simples, já foi dada no enunciado:
Já a integral da direita requer um pouquinho de criatividade. Veja que o enunciado diz que:
Distribuindo o integrando:
Logo:
Do enunciado, tiramos os valores das duas integrais mais a direita.
Passo 3
Opa! Agora já temos todos os valores que precisamos. Só substituir:
Que é exatamente a letra !
Resposta
Letra a.