(a) Seja
Calcule o volume do sólido obtido pela rotação de em torno da reta .
(b) Calcule a área da região formada pelos pontos tais que está entre
Passo 1
(a)
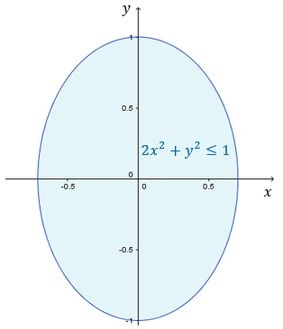
Vamos começar esboçando a região .
O conjunto é composto por todos os pontos que estão dentro da elipse .
Vejamos onde essa elipse cruza os eixos coordenados:
Então aqui está o conjunto :
Passo 2
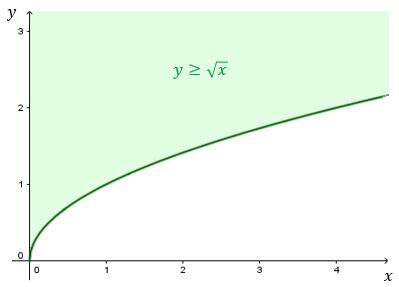
A outra restrição da região é .
Repare que isso nos dá uma informação muito importante: não está definida para , portanto, na região , devemos ter obrigatoriamente .
E aqui está o esboço da região :
Passo 3
é a interseção das regiões e :
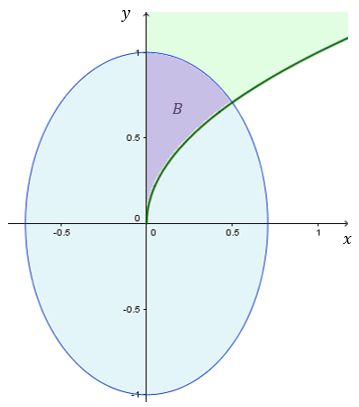
Passo 4
Agora que conseguimos visualizar a região, podemos pensar em como montar a integral que vai nos dar o volume do sólido de revolução.
A região é limitada por duas curvas, então vamos usar o método dos anéis circulares.
Mas pra montar as integrais precisamos descobrir onde as curvas se interceptam! Então vamos fazer isso:
Então temos
Mas como , então o ponto de interseção é em , o que faz sentido, olhando a figura.
Então os limites de integração na nossa integral do volume vão ser e , beleza?
Passo 5
Agora fica a questão: qual vai ser a função dentro da nossa integral?
Primeiramente, não podemos integrar né, temos que isolar o :
Passo 6
O volume do sólido de revolução vai ser:
onde e são os raios externo e interno, respectivamente.
Estamos fazendo a revolução em torno da reta , que fica acima da região . Então o raio externo é e o raio interno é :
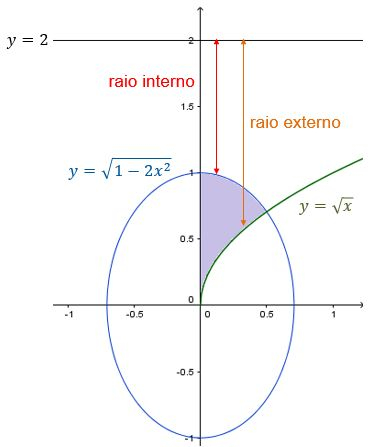
Então temos que
Pronto, finalmente montamos integral!
Agora ainda tem que calcular a bendita...
Passo 7
Antes de mais nada, vamos dar uma melhorada nesse integrando:
Desenvolvendo, isso vai dar:
Então o nosso volume vai ser:
Vamos separar isso em duas integrais, porque integrar vai dar um certo trabalho, enquanto o resto sai direto:
Passo 8
Vamos começar calculando:
Isso está com uma baita cara de substituição trigonométrica. Vamos fazer o seguinte:
Assim:
Também temos que escrever em função de :
Adaptando os limites de integração:
Passo 9
Então a integral ficou:
Lembrando que
Vamos ter:
Passo 10
A outra integral não vai dar tanto trabalho:
Agora é só simplificar essas frações todas:
Passo 11
Show, estamos quase acabando!
Lá no começo vimos que
E depois calculamos:
Então o volume vai ser:
Pronto, aí está a (linda) resposta da letra (a).
Passo 12
(b)
Agora ele está pedindo a área da região entre as funções e , com .
Felizmente todo o nosso trabalho da letra (a) vai ajudar aqui. Podemos reaproveitar o esboço da região pra ver como é essa nova região da letra (b).
Primeiramente, já sabemos onde as funções se cruzam: em .
Também sabemos que para , a função que está em cima, enquanto que para , que está em cima:
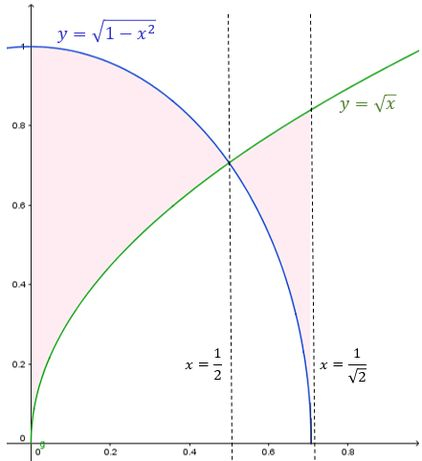
Então a área pedida vai ser dada por:
Passo 13
Pra não ficar confuso, vamos separar isso em 4 integrais:
A primeira nós já calculamos na letra (a):
Passo 14
A segunda integral vai ser:
Passo 15
Agora vamos pra terceira integral:
Cuidado pra não confundir, com essa :
Passo 16
Pra finalizar, a 4ª integral:
Vamos reaproveitar a substituição trigonométrica da letra (a):
Temos que a integral indefinida é:
Igualzinho a letra (a). A diferença agora está nos limites de integração:
Então nossa integral ficou:
Pra nos livrar desse sinal negativo, podemos inverter os limites de integração e escrever ela assim:
Passo 17
Então a 4ª integral vai dar:
Passo 18
Pronto, agora é só somar o resultado das 4 integrais pra obter a área:
O negócio já tá feio pra caramba, mas se quiser juntar os termos só pra ficar um pouco esteticamente mais agradável, fica:
AEE até que enfim acabamos esse capeta de questão!! :D

Resposta
(a)
(b)