Seja a região que está entre as curvas e no intervalo . Determine o volume do sólido obtido ao rotacionarmos em torno da reta .
Passo 1
Vamos desenhar essa região aí, só um seno (azul) e um cosseno (vermelho):
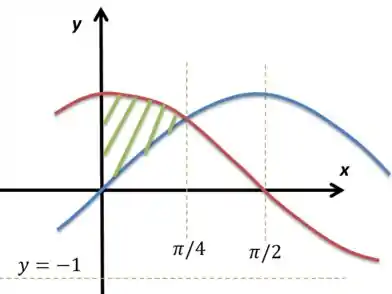
O que faremos aqui é girar a região pintada em verde em torno desse eixo também verde que passa por . Basta jogar na fórmula de cálculo de volume, reparando que faremos o gráfico do seno rotacionado menos a rotação do cosseno, já que o azul está mais distante desse eixo no intervalo pedido: