4. Encontre a derivada dada, encontrando as primeiras derivadas e observando o padrão que ocorre.
Passo 1
Oi, galerinha! Tudo bom? O enunciado pede para calcularmos
Isso significa derivar a função vezes. Poder, a gente até pode fazer isso, mas vai demorar muito tempo né.
Então vamos usar uma ajudinha que o próprio enunciado deu. Ele nos disse para encontrarmos as primeiras derivadas e observarmos um padrão.
Então bora fazer isso!
Passo 2
Fazendo as primeiras derivadas ficamos com,
Repara que a partir da quarta derivada, tudo volta a ser repetir. Então encontramos um padrão, onde a função se repete a cada ciclo de .
Então para saber qual é a derivada , vamos dividir esse valor por .
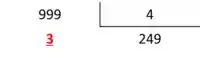
O nosso resultado é e o resto é . Agora vamos interpretar isso!
Para chegar na derivada , foram repetidos ciclos, mais . Ou seja, o nosso resultado é o mesmo da derivada número .
Logo, se tínhamos que
Temos que,
Prontinho! Mas, galerinha, se vc quiser tirar uma prova real. Pega uma derivada de ordem menor e calcula a derivada até lá. Depois pega a ordem da derivada e divide por , veja qual é o resto. Através do valor do resto, olha para o padrão que resolvemos e ve se bate. Belezinha?