Assinale a alternativa cuja afirmação é verdadeira
- Se é uma função derivável, com derivada contínua, tal que possui pontos críticos, então possui extremos locais.
- Se é uma função qualquer tal que , então existe tal que
- Se é uma função derivável, com derivada contínua, é o único ponto crítico de e é o ponto de mínimo local de então é o ponto de mínimo global de .
- Se é uma função contínua tal que é derivável em e , então existe tal que
- Se é uma função derivável tal que e para todo , então para todo
Passo 1
Pra gente resolver essa questão vamos ter que testar cada afirmativa uma a uma, beleza? Vamos começar com a letra . Será que ela é verdade?
Bem, a função tenta nos forçar a ideia de que todo ponto crítico é necessariamente um ponto de extremo (máximo ou mínimo). Dá uma olhada nessa função:
Pô, essa função tem sim um ponto crítico no intervalo proposto, o ! Mas veja bem:
Se a primeira derivada não muda de sinal nunca, quer dizer que é estritamente crescente (primeira derivada positiva). E nisso galera, já matamos a primeira alternativa: FALSA! Não dá pra ter extremos locais em funções estritamente crescentes, né não?
Passo 2
A letra nos dá uma quase verdade. Pensa comigo, se eu multiplico um valor negativo por outro positivo, dá negativo certo? Então se for positivo e for negativo, ou vice versa, necessariamente entre e existe um que zera a função. Caso contrário, os sinais de e não teriam como ser diferentes.
Só um detalhezinho galera, que torna essa letra falsa. A letra não fixa que é contínua! Então pode existir uma função descontínua como por exemplo...
...em que sem que exista uma raiz tal que e esteja entre e . Veja que nesse exemplo nem sequer existe um valor de que zere a função!
Passo 3
A letra está dizendo que se a minha função tem um único ponto crítico e ele é de mínimo, então esse é seu mínimo global. Bem, seja esse ponto de mínimo o ponto , pela definição de ponto mínimo, vamos ter:
Lendo isso, o que estamos dizendo é que no intervalo em que a função está definida, antes do ponto crítico, a função decresce e depois, a função cresce. Oras, e o que é isso se não a definição de um ponto de mínimo?
Agora, se esse ponto crítico é único no intervalo , significa que não existe nenhum outro ponto que zere a primeira derivada! E logo, a primeira derivada não muda de sinal em nenhum intervalo além dos enunciados.
Pô galera, se isso aí acontece, a função vai ser estritamente crescente em e estritamente decrescente em . Veja por exemplo a função:
Nesse caso, temos um único ponto crítico que é o próprio . E como a primeira derivada é uma reta que passa na origem, é válido:
Graficamente dá pra gente tirar uma ideia legal também:
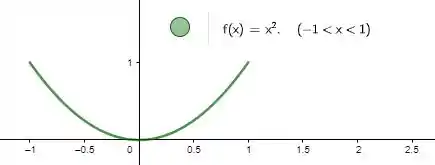
Então temos a nossa resposta certa! Demorou, bora pra próxima!
Passo 4
A letra está condicionando a existência de pontos críticos a um algebrismo. Bem, se então necessariamente . Só que o caminho que leva de até pode ser, por exemplo, estritamente crescente! Como uma reta por exemplo! Não precisa ter um ponto de máximo ou de mínimo no meio do caminho pra o segundo ponto estar mais alto que o primeiro!
A reta que casa algebricamente com o imposto é:
Perceba que:
Logo a reta não possui pontos críticos, a restrição imposta está satisfeita e de quebra vimos que o caminho pode ser sim estritamente crescente. Tudo abobrinha o que a letra disse!
Passo 5
Show, bora pra última letra. A diz que se a função é estritamente crescente nesse intervalo, algo que ela diz ao afirmar que , então ela ta necessariamente acima do eixo no intervalo, algo que ela diz ao afirmar que .
Oras, uma função pode ser crescente e estar abaixo do eixo ! Então é falso! Veja o exemplo:
Essa função é maior que somente pra . Ou seja, no intervalo , um intervalo pertencente ao intervalo , a função está abaixo do eixo ! E sendo uma reta cuja derivada é sempre positiva:
Então temos ai uma função estritamente crescente. Ah, e além disso, essa função em específico satisfaz:
Restrição imposta pelo enunciado. Fechamos então!