Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Diferenciabilidade

Ver Teoria
Exercício 251234567891011121314151617181920212223242627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3:

Sejam a ,   b ∈ R . Considere a função f : R → R definida por

f x = g x ,               s e       x < 1 h x ,               s e       x ≥ 1

onde

g x = a + ∫ - 1 x 2 t - 1   d t                                 e                               h x = ∫ - 1 x 3 - b t   d t

  1. Determine os valores de a e b para que a função f seja contínua e diferenciável.
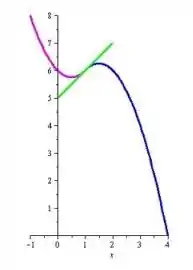
  2. Esboce abaixo o gráfico de f . Desenhe também a reta tangente ao gráfico de f no ponto 1 ,   f 1 .

Passo 1

a )

Bem, antes de nos preocuparmos com a teoria de diferenciabilidade e continuidade, por que não calculemos primeiro as integrais? Ora! Isso é totalmente possível, pois são integrais não muito complexas, veja:

g x = a + ∫ - 1 x 2 t - 1   d t

g x = a + 2 t 2 2 - t - 1 x =

a + 2 x 2 2 - x - 2 - 1 2 2 - - 1 =

g x = x 2 - x - 2 + a

Do mesmo Jeito, calculemos o h x !

Passo 2

h x = ∫ - 1 x 3 - b t   d t

Lembrando que b é constante...

h x = 3 t - b t 2 2 - 1 x =

h x = 3 x - b x 2 2 - - 3 - b 2 =

- b x 2 2 + 3 x + 3 + b 2

Passo 3

Bem, calculada as funções, podemos ir para a Teoria. Para a função ser contínua em x = 1 ,

g 1 = h 1

Então

1 2 - 1 - 2 + a = - b 1 2 2 + 3 1 + 3 + b 2

- 2 + a = 6  

a = 8

Descobrimos a , mas ainda falta nos o b , e para isso, vamos usar a condição de diferenciabilidade: uma função só é diferenciável se as derivadas forem contínuas naquele ponto...

g ' 1 = h ' 1

Derivando cada um das funções...

g x = x 2 - x - 2 + a       →           g ' x = 2 x - 1

h x = - b x 2 2 + 3 x + 3 + b 2       →         h ' x = - b x + 3

Então...

2 1 - 1 = - b 1 + 3     →

b = 2

Passo 4

b )

Com o a e o b definidos...

g x = x 2 - x - 2 + a   →

g x = x 2 - x + 6

h x = - b x 2 2 + 3 x + 3 + b 2   →

h x = - x 2 + 3 x + 4

Então a função f é...

f x = g x ,               s e       x < 1 h x ,               s e       x ≥ 1           →

f x = x 2 - x + 6 ,               s e       x < 1 - x 2 + 3 x + 4 ,               s e       x ≥ 1

Então quando x é menor que 1 , estamos falando de uma parábola com a concavidade pra cima. O vértice dela, você pode encontrar derivando...

g ' x v = 2 x v - 1 = 0               →               x v = 1 2

e y ...

y v = 1 4 - 1 2 + 6 = 23 4

A outra parábola, com a concavidade para baixo e vértices em

h ' x v = - 2 x v + 3 = 0         →           x v = 3 2

y v = 25 4

Então, o gráfico da função é...

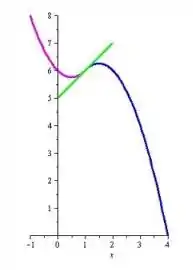
Resposta

a )       a = 8         e     b = 2

b )

Exercícios de Livros Relacionados

Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você
Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de
Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .
Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .
Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .