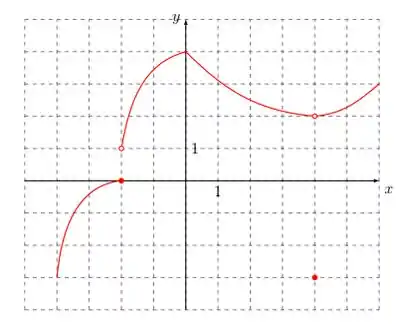
- Considere a função cujo gráfico está representado abaixo. Determine os pontos no intervalo em que não é diferenciável.
Passo 1
Oi, galerinha! Tudo bom? Aqui temos que dizer em quais pontos as função não é diferenciavel. E para isso precisamos lembrar quais critérios devem ser atendidos para função ser diferenciavel.
O primeiro é: funções que não são contínuas em um certo ponto, automaticamente, não são diferenciáveis nesse ponto.
Agora, se a função for contínua, ela pode ou não ser diferenciável, precisamos usar outro critério para avaliar: ela precisa ter suas derivadas laterais iguais e diferente de .
Agora vamos analisar o gráfico!
Passo 2
Olhando para o gráfico, de cara já conseguimos perceber que nossa função não é continua. Ou seja, nos pontos onde há descontinuidade a nossa função não será diferenciavel.
Então vamos buscar esses pontos:
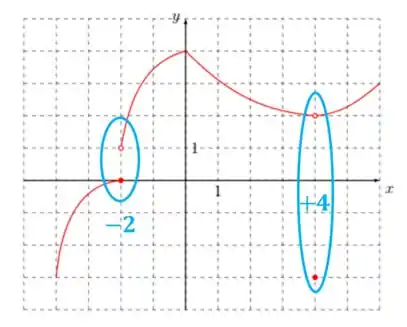
Sendo assim os pontos são pontos onde a função não é diferenciavel.
Passo 3
Além da descontinuidade, temos que avaliar os pontos onde as derivadas laterais são diferentes. Isso acontece quando a função muda de perfil, como é o caso do .
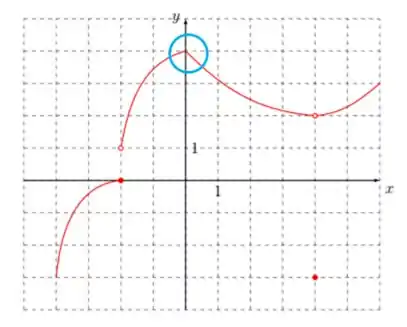
Para a derivada de temos uma função linear e para temos uma decaimento. Logo,