No exercício, cada figura mostra o gráfico de uma função em um intervalo fechado . Em que pontos do domínio a função parece ser
derivável?
contínua, mas não derivável?
nem contínua nem derivável?
Justifique sua resposta.
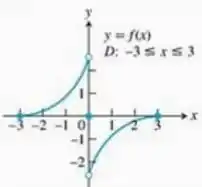
Passo 1
Para que a função seja derivável é preciso que ela seja contínua e que sua derivada exista.
Aparentemente, pelo desenho, o único ponto que não será derivável, por não ser contínuo, é ! Então a função é derivável em
onde é seu domínio de até .
Passo 2
Para que seja contínua e não-derivável a função deve ser, no ponto, contínua sem que a derivada exista. Como fora da descontinuidade de nós não temos nenhum ponto onde a derivada aparenta lateralmente divergir ou explodir para , temos que o único ponto não derivável é o , onde a função é descontínua.
Sendo assim, não há pontos onde é contínua mas não derivável.
Passo 3
Como, comentado na letra , o único ponto não derivável é , por ser descontínuo. Essa é nossa resposta!