USP, Sem Campus, Cálculo 1, Listas de C1 - Profª Michelle Pierri - 5ª Lista - Derivadas - Definição e Regras de Derivação, Questão 15
Seja . Verifique se é contínua e diferenciável em . Esboce o gráfico de .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar se a função , definida por partes, é contínua e diferenciável em . Pra isso, a gente precisa relembrar que uma função é dita contínua em um ponto se o limite da função naquele ponto existe, ou seja:
E se o valor desse limite é igual a função no ponto:
Um fato interessante sobre esse assunto é que funções que não são contínuas em um certo ponto, automaticamente não são diferenciáveis nesse ponto. Mas se a função for contínua, ela pode ou não ser diferenciável. Aí pra testar se a função é diferenciável no ponto, nós temos que testar se os limites laterais são iguais e se eles são diferentes de .
Então, antes de tudo, vamos ter que calcular os limites laterais de quando tende a pela direita e pela esquerda.
Vamos lá!
Passo 2
Para , calculando o limite pela esquerda quando , teremos:
Como não temos nenhuma restrição no domínio, podemos apenas substituir o valor do limite na função para obter:
Da mesma forma, pela direita teremos o limite:
Por definição, em nossa função assume o valor . Então, no ponto :
Dessa forma, nossa função é descontínua no ponto e, portanto, também não é diferenci��vel nesse ponto.
Vamos dar uma olhadinha no gráfico:
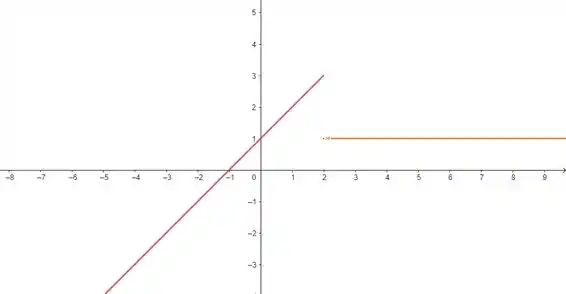
Percebe como há um “salto” na função em , sinal de que de fato há uma descontinuidade no ponto.
Valeu, galera! Até a próxima! 😉