Exercícios Resolvidos de Diferenciabilidade

Ver Teoria

Exercício 99 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 100

Enunciado

UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 5, Questão 6

Mostre que se é derivável em e,

então o coeficiente angular da reta normal ao gráfico de em é

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc1!!! Nosso objetivo é mostrar que o coeficiente angular da reta normal a um ponto de uma função é dada por

Passo 2

Para fazermos essa questão vamos desenhar duas retas ortogonais no plano cartesiano

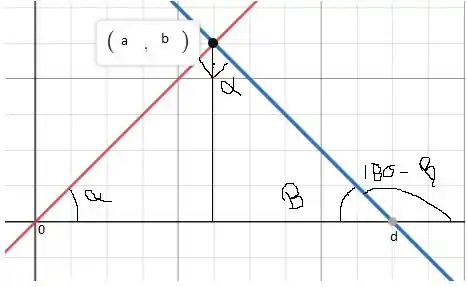
Temos que os coeficientes angulares das retas vermelha e azul são, respectivamente, iguais à

Mas usando identidades trigonométricas. Temos que

Agora, ao olharmo nossa figura, temos que

Logo, temos que

Portanto,

Agora, como o coeficiente angular da reta tangente ao ponto da função é dada por

Podemos concluir que o coeficiente angular da reta perpendicular a reta tangente nesse ponto é

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Exercícios de Livros Relacionados

Faça o gráfico da função f x = x + x . Dê um zoom primeiro em direção ao ponto (-1,0) e então em direção a origem. Qual a diferença entre os comportamentos de f próximo a esses dois pontos? O que você

Lembre-se de que uma função f é chamada par se f - x = f ( x ) para todo x em seu domínio, e ímpar se f - x = - f ( x ) para cada um destes x . Demonstre cada uma das afirmativas a seguirA derivada de

Seja f : R → R uma função tal que quaisquer que sejam x e t f x - f t ≤ x - t 2 Calcule f ' x .

Suponha f definida em R , derivável em 0 e f 0 = 0 . Prove que existe g definida em R , contínua em 0 , tal que f x = xg x para todo x .

Sejam f e g definidas em R , com g contínua em 0 , e tais que, para todo x , f x = xg x . Mostre que f é derivável em 0 .