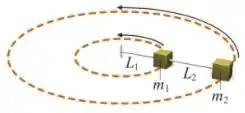
Q - Um bloco de massa está preso a um fio, de comprimento , que está fixo na outra extremidade. O bloco desloca-se num círculo horizontal, suportado por uma mesa sem atrito. Um segundo bloco, de massa , está ligado ao primeiro por um fio de comprimento e também se desloca num círculo, conforme mostrado na figura. Se os dois blocos giram com velocidade angular , a tensão no fio de comprimento , em Newtons, é:
Passo 1
Vamos para cima da questão com tudo!
Para achar a força de tensão (tensão no fio de comprimento )vamos fazer primeiro um diagrama de corpo livre dos blocos, para visualizar melhor a situação, temos o seguinte então:
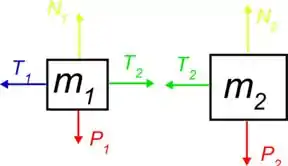
Para que os blocos possam girar, deve haver uma força resultante que aponte para o centro da circunferência que eles descrevem.
Essa força é conhecida como força centrípeta e é dada por:
Onde é a velocidade do corpo e é o raio da circunferência que o corpo descreve. Então tanto a força resultante em quanto em é iguala a força centrípeta, mas com valores diferentes para cada um.
Então podemos usar a segunda lei de Newton para avaliar o bloco e tentar isolar e calcular seu valor.
Vamos lá então!
Passo 2
Pela segunda lei de Newton para , temos que:
Usando que , temos que:
Então precisamos achar quem é .
Passo 3
Para achar vamos usar a segunda lei de Newton em e chagar em uma expressão para . Temos que:
Usando que , temos que:
Jogando isso na expressão que chegamos para no passo anterior, ficamos com:
Finalizado com sucesso nosso problema!