. Um avião aeromodelo (massa ) voa em um círculo horizontal de raio com velocidade escalar constante , preso a um fio ideal que exerce a força de tração , fazendo um ângulo de com a horizontal que passa pelo centro do avião. A força de sustentação aerodinâmica faz um ângulo de com a vertical que passa no centro do avião. A figura abaixo mostra as forças que atuam sobre o avião. Determine e a tração do fio .

Passo 1
Vem comigo e vamos juntos atrás da solução desse problema!
Para começarmos bem esse problema, vamos desenhar o diagrama de corpo livre desse avião. Temos:
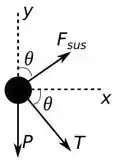
Para encontrarmos a força de sustentação e a força de tração, o melhor caminho que podemos fazer é usar a segunda lei de Newton ao nosso favor.
Como o avião realiza um movimento circular, a força resultante na direção tem que ser igual a força centrípeta, dada por:
E como ele não varia a sua altura quer dizer que a força resultante na direção é igual a zero.
Vamos então fazer essas análises.
Passo 2
Na direção , temos o seguinte:
Usando que , temos:
Guarda isso que vai ser útil.
Passo 3
Agora vamos analisar a direção , temos:
Agora vamos substituir o que encontramos para no passo anterior, assim:
Agora vamos isolar , temos:
Substituindo os valores que conhecemos, temos:
Com isso temos que:
Passo 4
Agora que temos o valor de , podemos encontrar o valor de usando a equação que chegamos no passo , assim:
Com isso temos que: