Em , um bloco de massa está inicialmente em repouso sobre um plano horizontal e conectado a uma barra rígida de massa desprezível e comprimento que pode girar em torno do ponto O. Um torque é então aplicado à barra, tal que possui uma aceleração angular constante. Existe atrito entre e a superfície horizontal, tal que os coeficientes de atrito estático e cinético são, respectivamente e . Considere .
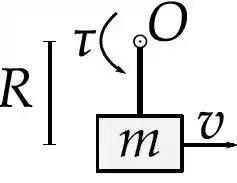
(c) Suponha agora que a barra rígida suporte uma tração máxima de . Qual é a maior velocidade da massa para que a barra não se rompa?
Passo 1
Primeiro de tudo...
Esse sistema está num plano horizontal. Ou seja, é como se isso estivesse girando horizontalmente em cima de uma mesa, por exemplo.
Essa seria uma imagem da gente olhando a mesa por cima:
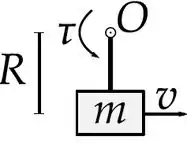
Beleza, entendemos isso.
Passo 2
Na letra (c), queremos a máxima velocidade do bloco para que a força de tração atinja o valor máximo.
Mas como assim?
Bom, a única força atuando na direção do centro da trajetória circular do bloco é essa força de tração da barra:
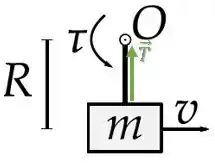
Então, essa força atua como uma força centrípeta no bloco:
Passo 3
Assim, basta substituir os valores e achar a que velocidade a força de tração atinge o valor de :
Resposta
(c)