Uma bola de massa está amarrada numa corda e gira descrevendo um círculo vertical com velocidade cujo módulo é constante e vale , como mostrado no diagrama abaixo. Em que ponto a corda tem maior probabilidade de quebrar, porque tem a maior tensão?

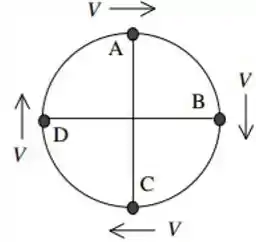
a) posição .

b) posição .

c) posição .

d) posição .

e) Nenhuma das alternativas anteriores.

Vamos fazer o diagrama das forças que atuam na bolinha em cada ponto e comparar a tensão da corda em cada um deles.

Muito bem, por se tratar de um movimento circular, sabemos que em todos os pontos terá uma resultante para o centro do circulo denominada força centrípeta.

Visto que a massa da bolinha, o Raio do circulo e a velocidade da bolinha são constantes em todos os pontos, a força centrípeta também será constante em todos os pontos.

Agora vamos analisar a força centrípeta em todos os pontos, ou seja, a resultante para o centro o circulo.

Nos pontos e , apenas a tensão da corda têm a direção do centro do círculo, logo:

No ponto , a força peso e a tensão na corda têm a direção e sentido para o centro do círculo, logo:

No ponto , a força peso e a tensão na corda têm a direção do centro do círculo, porém, sentidos opostos, logo:

Então comparando as tensões:

Logo a tensão será maior no ponto .