Uma caixa encontra-se sobre um carrossel, a uma distância do eixo de rotação. Inicialmente todo o sistema encontra-se em repouso. No instante o motor do carrossel é ligado e sua velocidade angular aumenta linearmente com o tempo, até atingir um valor máximo no instante , conforme mostrado na figura. Depois disso, a velocidade angular permanece constante neste valor máximo. Suponha que a caixa não escorregue em nenhum momento.
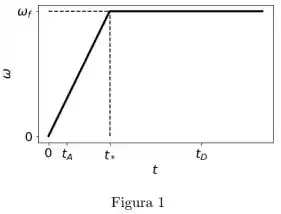
Suponha, agora, que em a caixa esteja na iminência de escorregar. Se , e , qual é o valor do coeficiente de atrito estático entre a caixa e o carrossel?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Após , o carrossel passa a girar com velocidade angular constante.
Assim, o movimento da caixa será um movimento circular uniforme. Logo, a força resultante na caixa será uma força apontando para o centro da trajetória, força centrípeta.
Mas quem é essa força?
A força de atrito né, pois é ela que está mantendo a caixa nessa trajetória circular junto do carrossel.
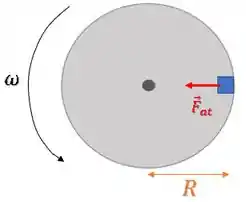
Passo 2
A força de atrito está atuando como centrípeta, então conseguimos descobrir seu valor igualando à expressão da força centrípeta:
Mas como temos informação sobre a velocidade angular em vez de , vamos usar a relação:
Substituindo:
Passo 3
Como a caixa está na iminência de deslizar, isso significa que a força de atrito estático está em seu valor máximo e com qualquer peteleco a mais a caixa passa a deslizar.
Então, podemos dizer que a vale:
Assim, temos:
Além disso, a caixa está em equilíbrio vertical, então:
Substituindo isso na expresão, temos:
Passo 4
Vamos jogar os valores numéricos e correr pro abraço.
Ficamos com a letra (f).
Resposta
Letra (f)