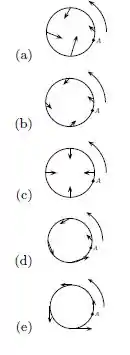
Um carro pequeno parte do repouso no ponto e segue uma trajetória circular, no sentido anti-horário, como indicado na figura. O módulo de sua velocidade aumenta a uma taxa constante. A alternativa que melhor representa o vetor aceleração nas diferentes posições da primeira volta é:
Passo 1
O primeiro passo aqui é lembrar que em todo movimento curvo, existe uma aceleração que aponta para o centro da trajetória (e por isso é perpendicular a trajetória no ponto) que se chama aceleração centrípeta, lembra dela?
Certo. Agora analisando o enunciado, vemos que ele nos diz que o carro tem o módulo da sua velocidade aumentando a uma taxa constante. O que isso quer dizer? Isso nos diz que existe uma outra componente que está na mesma direção do movimento, ou seja, sempre tangente à circunferência.
O que podemos tirar dessas duas informações? Que a nossa aceleração resultante está inclinada e as duas componentes são perpendiculares entre si.
Passo 2
Agora, como podemos medir o módulo dessas acelerações? O enunciado não nos dá os dados para tirarmos os valores exatos, mas sabemos que a aceleração centrípeta possui a seguinte expressão:
Onde é a velocidade tangencial. Lembra que esta velocidade aumenta à uma taxa constante? Vamos chamar esta taxa de , beleza? Então:
Substituindo, temos:
Como e são constantes, temos que a aceleração centrípeta cresce com o tempo!
Isso nos diz que a componente tangencial da aceleração se mantém constante(igual a ) e a aceleração centrípeta cresce com o tempo.
A afirmativa que mais se adequa a essas condições é a letra (a).
Resposta
(a)