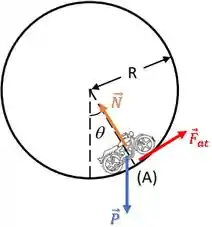
A figura mostra um motociclista que precorre um Globo da Morte de raio sem deixar de estar em contato com o mesmo. No ponto (A) que faz um ângulo com a vertical, sua velocidade é e se mantém constante. A massa da moto e motociclista é .
(a) Faça o diagrama de corpo isolado da motocicleta no ponto (A).
(b) Suponha que e e calcule o módulo da força normal no ponto (A), .
(c) Suponha que no ponto (A) a força de atrito estática com o solo atinge seu valor máximo. Use o resultado do item anterior para calcular o coeficiente de atrito estático .
Passo 1
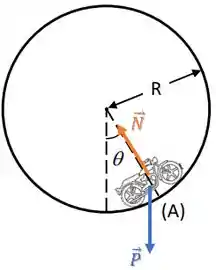
Na letra (a), queremos as forças atuando sobre a moto.
Temos a força peso que sempre aponta para baixo e a força normal que aponta na direção perpendicular à superfície da rampa:
Só essas?
Na verdade, se só existem essas forças, a moto estaria desacelerando devido à componente da força peso que atua no sentido contrário ao movimento.
Então, para que a moto mantenha sua velocidade constante, deve haver uma força de atrito empurrando ela “para frente”:
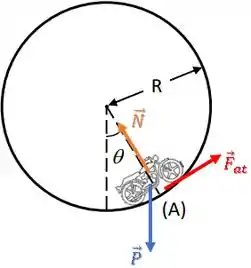
Ué, mas força de atrito para frente???
Isso mesmo!
Quando o motociclista acelera a moto, o que acontece é que as rodas tentam girar mais rápido no sentido horário. Assim, a força de atrito aparece contra essa tendência de deslizamento empurrando a moto para frente.
Passo 2
Ne letra (b), queremos o módulo da força normal no ponto A.
Como a moto realiza uma trajetória circular, a força resultante na direção radial (apontando para o centro) deve ser igual à resultante centrípeta:
Passo 3
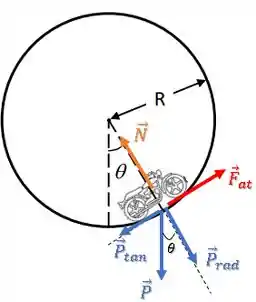
Para analisar as forças na direção radial, temos que decompor o vetor peso que apresenta uma componente em cada eixo (radial e tangencial).
Para isso, vamos usar o ângulo .
Vamos transportar o ângulo para o ponto de aplicação da força peso, traçando os eixos radial e tangencial:
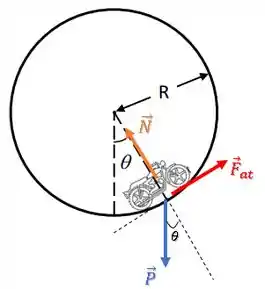
Decompondo a força, temos:
Passo 4
Agora, vamos fazer o somatório de forças na direção radial:
A resultante deve apontar para o centro da trajetória circular, então vamos considerar o sentido apontando para o centro como positivo (sentido da aceleração):
Passo 5
A força centrípeta tem uma expressão igual a:
Aplicando essa expressão, temos:
Temos ainda que a componente vale:
A força peso é massa vezes aceleração da gravidade:
Colocando em evidência a massa:
Passo 6
Substituindo os valores numéricos, temos:
Passo 7
Na letra (c), queremos o coeficiente de atrito estático sendo que a força de atrito está em seu valor máximo.
Força de atrito estático? Mas a moto não está em movimento??
Sim, a moto está em movimento, porém os pneus da moto estão girando sem deslizar no solo. Como não há deslizamento, o atrito é estático.
Quando a força de atrito estático atinge seu valor máximo, temos que ela vale:
Nós já temos o valor da força normal , mas ainda falta o valor da .
Passo 8
Vamos aplicar a Segunda Lei de Newton na direção tangencial, agora.
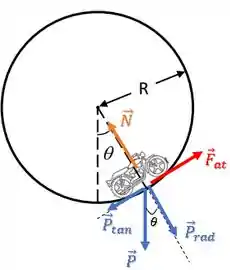
Como a moto está com velocidade constante, temos um equilíbrio de forças na direção tangencial:
Passo 9
Voltando à expressão da , temos:
Substituindo os valores, temos:
Resposta
(a)
(b)
(c)