Quatro partículas idênticas descrevem movimentos circulares concêntricos, em um plano horizontal, e estão conectadas entre si através de fios ideais do mesmo tipo, conforme a figura. Aumenta-se a frequência angular da rotação gradativamente. Nestas condições, o fio que se arrebenta primeiro é o de número
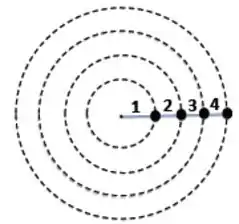
(a) 1
(b) 2
(c) 3
(d) 4
(e) 1, 2, 3 e o 4 simultaneamente
Passo 1
Essa é aquela questão que a gente não sabe nem por onde começar direito. Antes de sair chutando, vamos pensar no seguinte: o fio que vai arrebentar primeiro é o que tiver a maior tensão, certo?
E aplicando a 2ª lei de Newton e umas fórmulazinhas da rotação deve dar pra gente achar as tensões em cada fio!
Então esse vai ser o raciocínio! ;)
Passo 2
Antes de começar, vou fazer umas considerações:
- As partículas são idênticas, então vamos dizer que elas têm todas massa .
- As partículas estão conectadas, rodando juntas, então elas têm a mesma velocidade angular .
- O raio do movimento é diferente pras partículas 1, 2, 3 e 4, então vou chamá-los, respectivamente, de , , e .
- Da mesma forma, podemos chamar as tensões dos fios de e . Isso vai ficar mais claro mais pra frente :)
Dito isso, vamos continuar!
Passo 3
Vamos começar isolando a partícula 4, já que só tem um fio ligado nela!
No plano horizontal (da figura), a única força atuando na partícula é a tensão do fio :
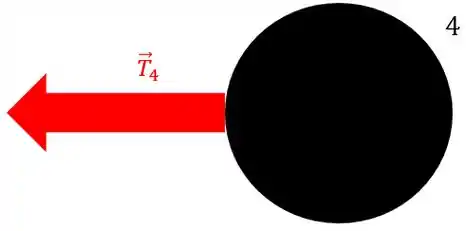
Passo 4
Então a força resultante na direção centrípeta é . E pela 2ª lei de Newton,
sendo a aceleração centrípeta da partícula. Ou seja,
Em módulo, isso fica:
Passo 5
O módulo da aceleração centrípeta é dado por:
Usando a relação , e lembrando que pra partícula 4 o raio é , isso fica:
Logo,
Passo 6
Show, vamos pra partícula ! Agora tem 2 fios, realizando 2 forças de tensão. A que aponta pro centro, no fio 3, é a .
Vamos ver o fio 4. Como ele é ideal, a tensão nele é sempre igual, então a tensão que aponta pra fora nada mais é que ! Saca só:
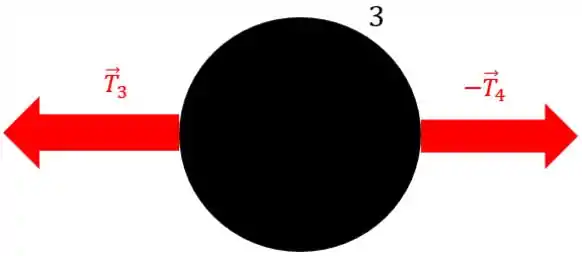
Passo 7
Vamos proceder exatamente da mesma maneira que pra partícula 4! Pela 2ª lei de Newton,
Passo 8
Agora, o raio do movimento é , então o módulo da aceleração centrípeta é:
Passo 9
Ótimo, vamos pra partícula 2! Vai ser bem parecido com a partícula 3!
As forças atuando nela no plano são as tensões dos fios , no fio 2, apontando pro centro do movimento, e , no fio 3, apontando pra fora:

Passo 10
Novamente, pela 2ª lei de Newton:
Passo 11
Pra partícula 2, o módulo da aceleração centrípeta é:
Então o módulo da tensão é:
Já tá dando pra ver um padrão né? Tipo .
Enfim, só falta a partícula 1 mesmo, então vamos calcular a tensão do fio 1 que nem a gente fez pros outros!
Passo 12
Da mesma maneira que pras outras partículas, temos uma tensão apontando pro meio da trajetória, e outra tensão apontando pra fora:

Passo 13
Aplicando a 2ª lei de Newton pela última vez:
Passo 14
Dessa vez o raio do movimento é , então:
O resultado foi que nem a gente suspeitou antes!
Passo 15
Recapitulando, obtivemos:
Portanto,
A tensão no fio 1 é maior, então ele arrebenta primeiro.
Resposta
Alternativa (a)