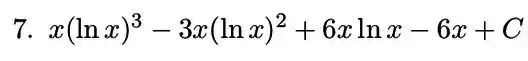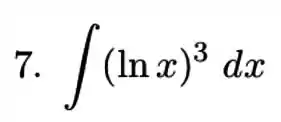
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 201123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Lá vamos nós para mais uma integral por partes. Aqui, vamos fazer

u = ln ⁡ x 3  

d v = d x

Então

d u = 3 ln ⁡ x 2 x   d x

E

v = x

Passo 2

Agora vamos substituir isso na expressão da integral por partes

∫ u   d v = u v - ∫ v   d u

∫ ln ⁡ x 3 d x = ln ⁡ x 3 x - ∫ x   3 ln ⁡ x 2 x   d x    

∫ ln ⁡ x 3 d x = ln ⁡ x 3 x - 3 ∫   ln ⁡ x 2   d x  

Passo 3

E agora? Para resolver a integral

∫   ln ⁡ x 2   d x  

Vamos precisar fazer de novo a integral por partes

u 2 = ln ⁡ x 2

d v 2 = d x

Então

d u 2 = 2 ln ⁡ x x d x

E

v 2 = x

Aplicando na integração por partes

∫   ln ⁡ x 2   d x   = ln ⁡ x 2 x - ∫ x 2 ln ⁡ x x d x  

∫   ln ⁡ x 2   d x   = ln ⁡ x 2 x - 2 ∫ ln ⁡ x d x

Passo 4

Estamos pensando a mesma coisa? É isso mesmo? Siiiim , mais uma integral por partes. Calma! É a ultima!

∫ ln ⁡ x d x

u 3 = ln ⁡ x

d v 3 = d x

Então

d u 3 = 1 x d x

E

v 3 = x

Aplicando na integração por partes

∫ ln ⁡ x   d x   = ln ⁡ x   .   x - ∫ x 1 x d x  

∫ ln ⁡ x   d x   = ln ⁡ x   . x - ∫ d x

∫ ln ⁡ x   d x   = x ln ⁡ x - x

Passo 5

Agora é só substituir as expressões que encontramos uma dentro na outra

∫ ln ⁡ x 3 d x = ln ⁡ x 3 x - 3 ∫   ln ⁡ x 2   d x  

∫   ln ⁡ x 2   d x   = ln ⁡ x 2 x - 2 ∫ ln ⁡ x d x

∫ ln ⁡ x   d x   = x ln ⁡ x - x

∫ ln ⁡ x 3 d x = ln ⁡ x 3 x - 3 ln ⁡ x 2 x - 2 x ln ⁡ x - x

∫ ln ⁡ x 3 d x = ln ⁡ x 3 x - 3 ln ⁡ x 2 x + 6 x ln ⁡ x - x

∫ ln ⁡ x 3 d x = x ln ⁡ x 3 - 3 x ln ⁡ x 2 + 6 x ln ⁡ x - 6 x + C

Não esquece da constante de integração!

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x