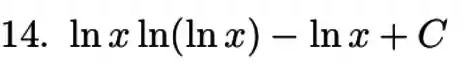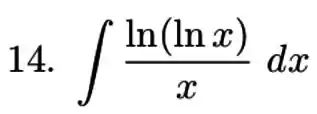
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração por Partes

Ver Teoria
Exercício 103123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Para usar aqui a técnica de integração por partes, precisamos primeiro fazer uma substituição para simplificar, olha só

u = ln ⁡ x

d u = 1 x d x

Então

∫ ln ⁡ ln ⁡ x x d x = ∫ ln ⁡ u   d u

Passo 2

Feita nossa substituição, agora podemos começar a aplicar a integração por partes. Cuidado! Não vamos confundir o u da integração por partes com a nossa substituição. Para não dar confusão vamos chamar o da integração por partes de u 2 ok?

u 2 = ln ⁡ u

d v = d u

Então

d u 2 = 1 u d u

v = u

Passo 3

Agora falta aplicar na expressão da integração por partes

∫ u 2   d v = u 2 v - ∫ v   d u 2

∫ ln ⁡ u = ln ⁡ u .   u   - ∫ u 1 u d u

∫ ln ⁡ u = u  ln ⁡ u   - ∫ d u

∫ ln ⁡ u = u ln ⁡ u   - u

Passo 4

Finalmente, só falta desfazer a substituição do passo 1.

u = ln ⁡ x

∫ ln ⁡ ln ⁡ x x d x = ∫ ln ⁡ u   d u

∫ ln ⁡ ln ⁡ x x d x = ln ⁡ x ln ⁡ ln ⁡ x - ln ⁡ x + C

Não esquece de colocar a constante de integração, viu?

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int_()^() z^3 e^z d z
Calcule a integral.int_()^() (x e^(2 x))/((1 + 2 x)^2) d x
Use a tabela de integrais ao final do livro para calcular as integrais 20 - ∫ t g - 1 x x 2d x
Primeiro faça uma substituição e então use integração por partes para calcular a integral. ∫ t 3e - t 2d t
Calcule a integral.int_0^(pi) x^3 cos x d x