UnB. Cálculo 1. Prova P3. 2021.1. Questão 1.
Responda os itens com respeito à integral
a) Utilize a fórmula de integração por partes fazendo e e determine o valor da integral.
b) Utilize a fórmula de integração por partes fazendo e e comente por que essa escolha não é boa.
c) A integral representa o volume de um sólido gerado pela de revolução de uma região, em torno do eixo . Descreva as curvas que delimitam essa região no plano.
Passo 1
Iae, meus queridos! Tudo certinho?
Muito bacana essa questão onde vamos trabalhar com integral por partes e vamos ver como é importante ter um bom feeling na hora de escolher as partes e da nossa integral.
Para essa questão, temos que calcular a integral por meio do método de integração por partes, onde
No item a) vamos considerar , e calcular a integral .
Tendo e , vamos calcular e
Substituindo os valores que calculamos na formula da integral por partes, temos
Substituindo nos intervalos de integração
Passo 2
No item b) vamos considerar , .
Tendo e , vamos calcular e
Substituindo os valores que calculamos na formula da integral por partes, temos
Embora tenhamos chegado no mesmo valor final, o percurso foi mais trabalhado, já que a integral deu mais trabalho de ser resolvida por não ter uma solução trivial, como no item a). Portanto essa escolha das partes de integração não é muito bacana.
Passo 3
No item c) a função a ser revolucionada em torno do eixo , é , como vemos em sua demonstração em duas dimensões.
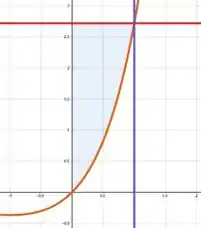
Com o variando de a e o variando de a , formando uma figura assim após a revolução
Algo parecido com o bico de um avião, que vai da origem do sistema até o plano
É isso! Entendeu tudo? Responde Aí! 😎👍
Resposta
a) .
b) Não é bacana por se tratar de um caminho mais trabalhoso para resolver a integral.
c) Imagem no passo-a-passo.