Considere que uma corda esticada está oscilando na direção vertical (y) por conta de uma onda harmônica que viaja ao longo da direção horizontal (x).
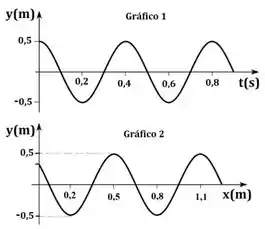
Os gráficos ao lado mostram a posição vertical de um certo elemento de corda em função do tempo (Gráfico 1) e o perfil da onda que está se propagando na corda, em um determinado instante de tempo, em função da posição horizontal (Gráfico 2). Sendo assim, quais são a velocidade da onda, , e a velocidade máxima de um certo elemento de corda, , em unidades de m/s ?
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
Passo 1
Precisamos descobrir que informações podemos tirar desses gráficos!
De qualquer um deles, temos que a amplitude, o valor máximo de é
Do gráfico 1 (y em função do tempo) podemos tirar o tempo de uma oscilação completa, o período:
Do gráfico 2 (y em função da posição) podemos tirar o espaço percorrido para um oscilação completa, o comprimento de onda (máximo a máximo ou mínimo a mínimo):
Passo 2
Para calcular a podemos lembrar da principal relação de uma onda:
Então,
Passo 3
Para calcular a velocidade máximo de um ponto da onda, a velocidade transversal, temos que lembrar que uma onda é descrita por um seno ou coseno da seguinte forma:
Então sua velocidade transversal será
Então a velocidade transversal máxima vai ocorrer quando o seno for máximo ou mínimo ():
Resposta
b) ,